3.3.1.- Descomposición de la suma de cuadrados total

El nombre análisis de varianza se deriva de la partición de la variabilidad total en sus partes componentes. La suma de cuadrados total corregida.

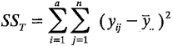
se usa como una medida de la variabilidad global de los datos. Intuitivamente, esto es razonable porque, si 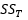tuviera que dividirse por el número apropiado de grados de libertad (en este caso, an -1 =N -1), se obtendría la varianza muestral de las y. La varianza muestral es, desde luego, una medida estándar de variabilidad.

Observe que la suma de cuadrados total corregida 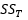se puede escribir como:

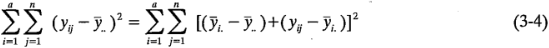
ó

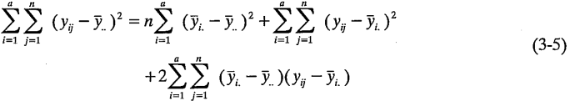
Sin embargo, el término del producto cruzado de la ecuación 3-5 es cero, ya que:

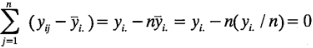
Se tiene, por lo tanto:

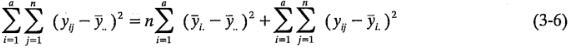
La ecuación 3-6 establece que puede hacerse la partición de la variabilidad total de los datos, medida por la suma de cuadrados total corregida, en una suma de cuadrados de las diferencias entre los promedios de los tratamientos y el gran promedio, más una suma de cuadrados de las diferencias de las observaciones dentro de los tratamientos y el promedio de los tratamientos. Entonces, la diferencia entre los promedios de los tratamientos observados y el gran promedio es una medida de las diferencias entre las medias de los tratamientos, mientras que las diferencias de las observaciones dentro de un tratamiento y el promedio del tratamiento, pueden deberse únicamente al error aleatorio. Por lo tanto, la ecuación 3-6 puede escribirse simbólicamente como:

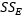Donde a se le llama la suma de cuadrados debida a los tratamientos (es decir, entre los tratamientos), y a  se le llama la suma de cuadrados debida al error (es decir, dentro de los tratamientos). Hay an = N observaciones en total; por lo tanto, 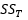tiene N-1 grados de libertad. Hay  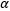niveles del factor (y medidas de  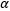tratamientos), de donde  tiene 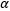 -1 grados de libertad. Por último, dentro de cualquier tratamiento hay n réplicas que proporcionan n - 1 grados de libertad con los cuales estimar el error experimental. Puesto que hay  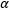tratamientos, se tienen a(n - 1) =an - a =N - a grados de libertad para el error.

Es útil examinar explícitamente los dos términos del lado derecho de la identidad fundamental del análisis de varianza (ecuación 3-6). Considere la suma de cuadrados del error:

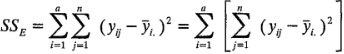
En esta forma es fácil ver que el término entre corchetes, si se divide por n -1, es la varianza muestral del tratamiento i-ésimo, o:

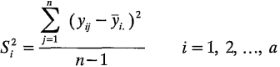
Ahora pueden combinarse a varianzas muestrales para obtener una sola estimación de la varianza poblacional común de la siguiente manera:

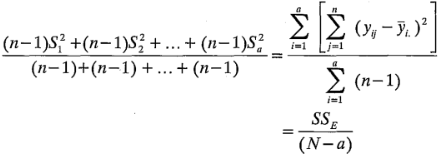
Por lo tanto,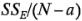 es una estimación combinada de la varianza común dentro de cada uno de los  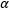tratamientos.

De manera similar, si no hubiera diferencias entre las medias de los a tratamientos, podría usarse la variación de los promedios de los tratamientos y el gran promedio para estimar 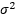. Específicamente: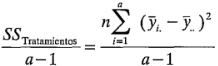

es una estimación de 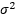si las medias de los tratamientos son iguales. La razón de esto puede verse de manera intuitiva de la siguiente manera. La cantidad 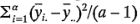estima 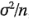, la varianza de los promedios de los tratamientos, de donde  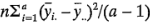debe estimar  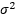si no hay diferencias en las medias de los tratamientos.

Se observa que la identidad del análisis de varianza (ecuación 3-6) nos proporciona dos estimaciones de 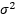: una basada en la variabilidad inherente dentro de los tratamientos y una basada en la variabilidad entre los tratamientos. Si no hay diferencias en las medias de los tratamientos, estas dos estimaciones deberán ser muy similares, y si no lo son, se sospecha que la diferencia observada puede ser causada por diferencias en las medias de los tratamientos. Aun cuando se ha usado un razonamiento intuitivo para desarrollar este resultado, puede adoptarse un enfoque un tanto más formal.

A las cantidades:

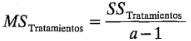
y

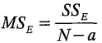
se les llama cuadrados medios. Se examinarán ahora los valores esperados de estos cuadrados medios. Considere:

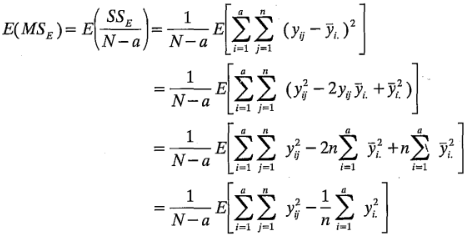
Al sustituir el modelo (ecuación 3-1) en esta ecuación se obtiene:

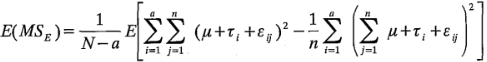
Entonces, al elevar al cuadrado y tomar el valor esperado de la cantidad entre corchetes, se observa que los términos que incluyen a 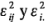 son reemplazados por  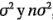respectivamente, debido a que 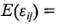0. Además, todos los productos cruzados que incluyen a 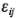tienen valor esperado cero. Por lo tanto, después de elevar al cuadrado y tomar el valor esperado, la última ecuación se convierte en:

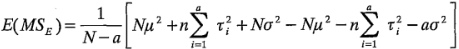
ó

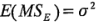
Aplicando un enfoque similar puede demostrarse también que:

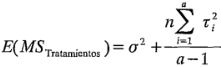
Por lo tanto, como se argumentó heurísticamente, 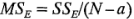 estima  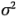y, si no hay diferencias en las medias de los tratamientos (lo cual implica que 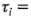0), 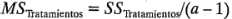 también estima 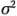. Sin embargo, observe que, si las medias de los tratamientos difieren, el valor esperado del cuadrado medio de los tratamientos es mayor que .

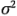Parece claro que es posible realizar una prueba de la hipótesis de que no hay diferencias en las medias de los tratamientos comparando . Se considera ahora cómo puede hacerse esta comparación.