3.3.2.- Análisis estadístico

Se investiga ahora cómo puede llevarse a cabo una prueba formal de la hipótesis de que no hay diferencias en las medias de los tratamientos (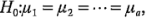o de manera equivalente, 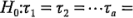0). Puesto que se ha supuesto que los errores  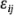siguen una distribución normal e independiente con media cero y varianza 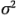, las observaciones  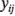tienen una distribución normal e independiente con media 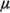+ 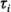y varianza 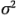. Por lo tanto,  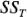es una suma de cuadrados de variables aleatorias con una distribución normal; por consiguiente, puede demostrarse que  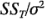tiene una distribución ji-cuadrada con N -1 grados de libertad. 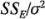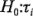Además, puede demostrarse que  es una variable ji-cuadrada con N -a grados de libertad y que  es una variable ji-cuadrada con a -1 grados de libertad si la hipótesis nula =0 es verdadera. 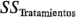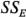Sin embargo, las tres sumas de cuadrados no son necesariamente independientes, ya que la suma de y  es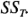. El siguiente teorema, que es una forma especial de un teorema El siguiente teorema, que es una forma especial de un teorema  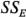y .

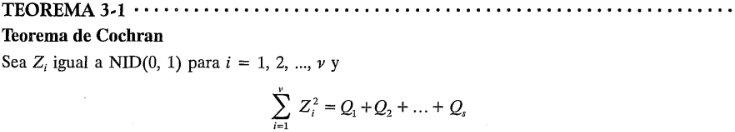
donde 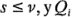tienen  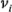grados de libertad 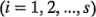. Entonces  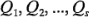son variables aleatorias ji-cuadrada independientes con  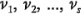grados de libertad, respectivamente, si y sólo si:

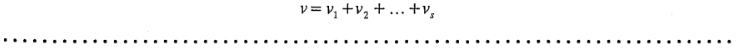
Puesto que los grados de libertad de 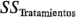 y 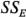 suman N-1, el número total de grados de libertad, el teorema de Cochran implica que  y 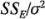 son variables aleatorias ji-cuadrada con una distribución independiente. Por lo tanto, si la hipótesis nula de que no hay diferencias en las medias de los tratamientos es verdadera, el cociente:

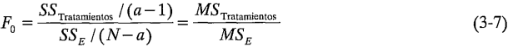
se distribuye como F con a - 1 y N - a grados de libertad. La ecuación 3-7 es el estadístico de prueba para la hipótesis de que no hay diferencias en las medias de los tratamientos.

Por los cuadrados medios esperados se observa que, en general, 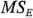 es un estimador insesgado de 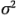. Asimismo, bajo la hipótesis nula,  es un estimador insesgado de 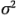. Sin embargo, si la hipótesis nula es falsa, el valor esperado de  es mayor que 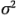. Por lo tanto, bajo la hipótesis alternativa, el valor esperado del numerador del estadístico de prueba (ecuación 3-7) es mayor que el valor esperado del denominador, y  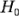deberá rechazarse para valores del estadístico de prueba que son muy grandes. Esto implica una región crítica de una sola cola superior. Por lo tanto,  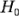deberá rechazarse y concluirse que hay diferencias en las medias de los tratamientos si:

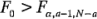
donde 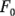 se calcula con la ecuación 3-7. De manera alternativa, podría usarse el enfoque del valor P para tomar una decisión.

Es posible obtener fórmulas para calcular estas sumas de cuadrados reescribiendo y simplificando las definiciones de 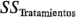 y 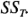 en la ecuación 3-6. Se obtiene así:

y

La suma de cuadrados del error se 'obtiene por sustracción como:

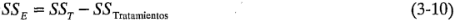
El procedimiento de prueba se resume en la tabla 3-3. Se le conoce como tabla del análisis de varianza.