3.4.3.- Gráfica de los residuales contra los valores ajustados

Si el modelo es correcto y se satisfacen los supuestos, los residuales deberán estar sin estructura; en particular, no deberán estar relacionados con ninguna otra variable, incluyendo la respuesta predicha. Una verificación simple es graficar los residuales contra los valores ajustados 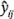. (Para el modelo de un experimento con un solo factor, recuerde que 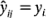, el promedio del tratamiento i-ésimo.) Esta gráfica no deberá mostrar ningún patrón obvio. En la figura 3-6 se grafican los residuales contra los valores ajustados para los datos de la resistencia a la tensión del ejemplo 3-1. No es evidente ninguna estructura inusual.

Un defecto que sale a relucir en ocasiones en esta gráfica es una varianza no constante. En ocasiones la varianza de las observaciones se incrementa cuando la magnitud de la observación se incrementa. Éste sería el caso si el error o ruido de fondo del experimento fuera un porcentaje constante de la magnitud de la observación. (Esto ocurre comúnmente con muchos instrumentos de medición; el error es un porcentaje de la escala de medición.) Si éste fuera el caso, los residuales se harían mayores conformes 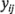 se hiciera más grande, y la gráfica de los residuales contra  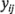se vería como un embudo o un megáfono con la boca hacia afuera. Una varianza no constante también surge en los casos en que los datos siguen una distribución no normal, sesgada, porque en las distribuciones sesgadas la varianza tiende a ser una función de la media.

Si se viola el supuesto de la homogeneidad de las varianzas, la prueba F sólo resulta afectada ligeramente en el modelo balanceado (el mismo tamaño de la muestra en todos los tratamientos) con efectos fijos. Sin embargo, en diseños no balanceados o en casos en que una de las varianzas es considerablemente más grande que las demás, el problema es más grave. Específicamente, si los niveles del factor que tienen las varianzas mayores corresponden también con los tamaños de las muestras más pequeños, el índice de error tipo I real es mayor que lo previsto (o los intervalos de confianza tienen niveles de confianza reales más bajos que los que fueron especificados). Recíprocamente, si los niveles del factor con las varianzas mayores tienen también los tamaños de las muestras mayores, los niveles de significación son mucho menores que lo anticipado (los niveles de confianza son más altos). Ésta es una buena razón para escoger tamaños de las muestras iguales siempre que sea posible. Para los modelos con efectos aleatorios, las varianzas del error diferentes pueden introducir alteraciones significativas en las inferencias sobre los componentes de la varianza, incluso cuando se usan diseños balanceados.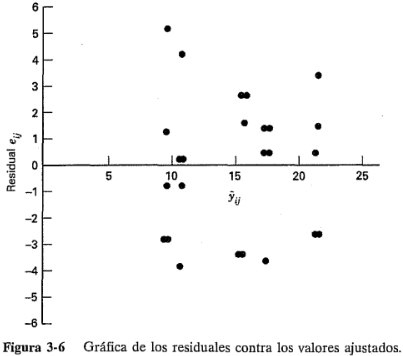

El enfoque usual para abordar el problema de una varianza no constante que ocurre por las razones expuestas antes consiste en aplicar una transformación para estabilizar la varianza para correr después el análisis de varianza en los datos transformados. En este enfoque, deberá tenerse presente que las conclusiones del análisis de varianza se aplican a las poblaciones transformadas.

Se han dedicado considerables esfuerzos de investigación a la selección de una transformación adecuada. Si los experimentadores conocen la distribución teórica de las observaciones, pueden hacer uso de esta información para elegir la transformación. Por ejemplo, si las observaciones siguen la distribución de Poisson, se usaría la transformación de la raíz cuadrada 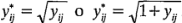. Si los datos siguen la distribución lognormal, la transformación logarítmica  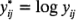es adecuada. Para datos binomiales expresados como fracciones, la transformación arcsen 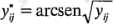es útil. Cuando no hay una transformación obvia, el experimentador realizará por lo general la búsqueda empírica de una transformación que iguale la varianza independientemente del valor de la media. Al final de esta sección se ofrecen algunos consejos al respecto. En los experimentos factoriales, los cuales se introducen en el capítulo 5, otro enfoque es seleccionar una transformación que minimice el cuadrado medio de las interacciones, siendo el resultado un experimento cuya interpretación es más sencilla. En el capítulo 14 se revisan con mayor detalle los métodos para seleccionar analíticamente la forma de la transformación. Las transformaciones que se hacen para la desigualdad de la varianza afectan también la forma de la distribución del error. En la mayoría de los casos, la transformación hace que la distribución del error esté más cerca de la distribución normal. Para más detalles sobre las transformaciones, referirse a Bartlett [7], Box y Cox [15], Dolby [38] y Draper y Hunter [39].

Pruebas estadísticas para la igualdad de la varianza

Aun cuando es frecuente el uso de las gráficas residuales para diagnosticar la desigualdad de la varianza, se han propuesto también varias pruebas estadísticas. Estas pruebas pueden considerarse como pruebas formales de las hipótesis:

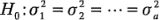
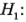 el enunciado anterior no es verdadero para al menos una .

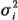Un procedimiento muy utilizado es la prueba de Bartlett. El procedimiento incluye el cálculo de un estadístico cuya distribución de muestreo está aproximada muy de cerca por la distribución ji-cuadrada con a - 1 grados de libertad cuando las a muestras aleatorias son de poblaciones normales independientes. El estadístico de prueba es:

donde:

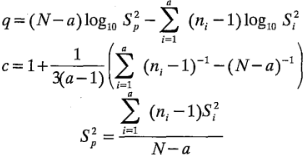
y 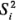 es la varianza muestral de la población i-ésima.

La cantidad q es grande cuando la diferencia entre las varianzas muestrales 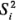es considerablemente grande, y es igual a cero cuando todas las 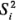son iguales. Por lo tanto, 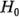deberá rechazarse para los valores de 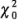que sean muy grandes; es decir, se rechaza 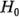sólo cuando:

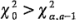
Donde 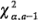 es el punto porcentual a superior de la distribución ji-cuadrada con a - 1 grados de libertad. También podría usarse el enfoque del valor P para tomar una decisión.

La prueba de Bartlett es muy sensible al supuesto de normalidad. Por consiguiente, cuando la validez de este supuesto está en duda, no deberá usarse la prueba de Bartlett.