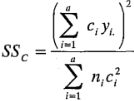3.5.4.- Contrastes

Muchos métodos de comparaciones múltiples utilizan el concepto de contraste. Considere el problema de la prueba de la fibra sintética del ejemplo 3-1. Puesto que se rechazó la hipótesis nula, se sabe que algunos pesos porcentuales del algodón producen resistencias a la tensión diferentes que otros, pero ¿cuáles son los que causan en realidad esta diferencia? Al principio del experimento podría sospecharse que los niveles 4 y 5 del peso porcentual del algodón (30 y 35 por ciento) producen la misma resistencia a la tensión, lo cual implicaría que la hipótesis por probar sería:

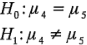
ó, de manera equivalente: 

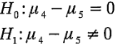
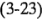
Si desde el principio del experimento se hubiera sospechado que el promedio de los niveles más bajos del peso porcentual del algodón (1 y 2) no difería del promedio de los niveles más altos del peso porcentual del algodón (4 Y5), entonces la hipótesis habría sido:

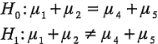
ó

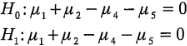
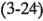
En general, un contraste es una combinación lineal de parámetros de la forma: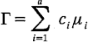

donde las constantes de los contrastes 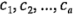 suman cero; es decir, 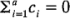. Las dos hipótesis anteriores pueden expresarse en términos de contrastes:

Las constantes de los contrastes para la hipótesis de la ecuación 3-23 son 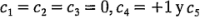=-1, mientras que para la hipótesis de la ecuación 3-24 son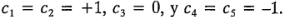 

Las pruebas de hipótesis que incluyen contrastes pueden hacerse de dos maneras básicas. En el primer método se utiliza la prueba . El contraste de interés se escribe en términos de los totales de los tratamientos, obteniéndose:

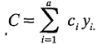
La varianza de C es:

cuando los tamaños de las muestras de cada tratamiento son iguales. Si la hipótesis nula de la ecuación 3-25 es verdadera, el cociente:

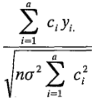
tiene la distribución N(0, 1). Entonces se sustituiría la varianza desconocida 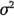 con su estimación, el error cuadrático medio  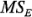y se utilizaría el estadístico:

para probar las hipótesis de la ecuación 3-25. La hipótesis nula se rechazaría si 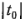 e la ecuación 3-27 excede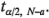 

En el segundo enfoque se utiliza la prueba F. Entonces, el cuadrado de una variable aleatoria t con v grados de libertad es una variable aleatoria F con un grado de libertad en el numerador y v grados de libertad en el denominador. Por lo tanto, puede obtenerse:

como un estadístico F para probarla ecuación 3-25. La hipótesis nula se rechazaría si 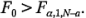 Este estadístico de prueba de la ecuación 3-28 puede escribirse como:

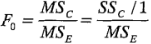
donde la suma de cuadrados de los contrastes con un solo grado de libertad es:

Intervalo de confianza para un contraste

En lugar de probar hipótesis acerca de un contraste, puede ser más útil construir un intervalo de confianza. Entonces el contraste suele expresarse en términos de los promedios de los tratamientos 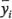. Suponga que el contraste de interés es:

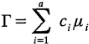
Al sustituir las medias de los tratamientos con los promedios de los tratamientos se obtiene:

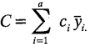
y

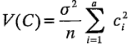
cuando los tamaños de las muestras son iguales. Si se usa 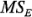 para estimar 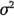, el intervalo de confianza de  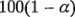por ciento para el contraste  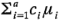es:

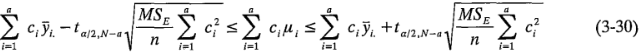
Evidentemente, si este intervalo de confianza incluye al cero, no podría rechazarse la hipótesis nula en fa ecuación 3-25.

Contraste estandarizado

Cuando hay interés en más de un contraste, con frecuencia es útil evaluarlos en la misma escala. Una forma de hacer esto es estandarizando el contraste para que su varianza sea 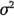. Si el contraste  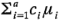se expresa en términos de los totales de los tratamientos como 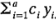, al dividirlo por  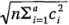se obtendrá un contraste estandarizado con varianza 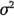. Entonces el contraste estandarizado es en realidad:

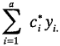
Donde:

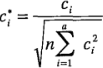
Tamaños de las muestras desiguales

Cuando los tamaños de las muestras de cada tratamiento son diferentes, se introducen modificaciones menores en los resultados anteriores. Primero, observe que la definición de un contraste requiere ahora que:

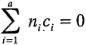
Otros cambios requeridos son directos. Por ejemplo, el estadístico t de la ecuación 3-27 queda como:

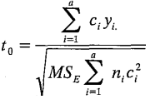
la suma de cuadrados de los contrastes de la ecuación 3-29 queda como: