Sea que 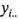 denote el total de observaciones bajo el nivel i-ésimo del factor 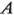, que 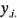 denote el total de observaciones bajo el nivelj-ésimo del factor 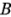, que 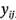 denote el total de observaciones de la celda ij-ésima, y que  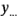denote el gran total de todas las observaciones. 

Se definen 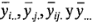 como los promedios correspondientes de los renglones, las columnas, las celdas y el gran promedio. Expresado matemáticamente, 


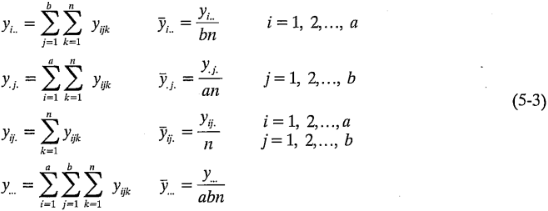
La suma de cuadrados total corregida puede escribirse como: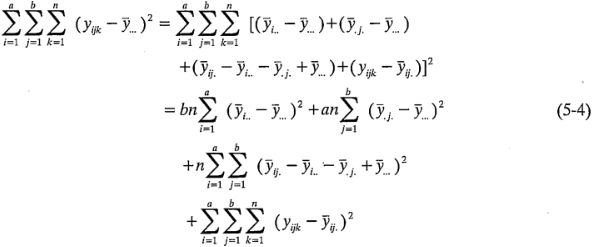

ya que los seis productos cruzados del lado derecho de la igualdad son cero. Observe que se ha hecho la partición de la suma de cuadrados total en una suma de cuadrados debida a "los renglones", o factor 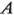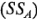; una suma de cuadrados debida a "las columnas", o factor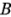 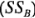; una suma de cuadrados debida a la interacción entre  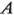y 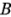 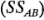; y una suma de cuadrados debida al error 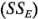. Por el último componente del lado derecho de la igualdad de la ecuación 5-4, se observa que debe haber por lo menos dos réplicas  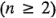para obtener una suma de cuadrados del error.

La ecuación 5-4 puede escribirse simbólicamente como:


El número de grados de libertad asociado con cada suma de cuadrados es:


Esta asignación de los 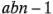 grados de libertad totales a las sumas de cuadrados puede justificarse de la siguiente manera: los efectos principales  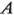y 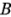 tienen  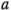y 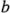 niveles, respectivamente; por lo tanto, tienen  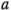-1 y 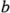-1 grados de libertad, como se indica. Los grados de libertad de la interacción son sólo el número de grados de libertad de las celdas (que es 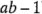) menos el número de grados de libertad de los dos efectos principales  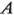y 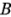; es decir, 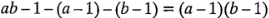. Dentro de cada una de las  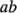celdas hay  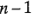grados de libertad entre las  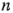réplicas; por lo tanto, hay  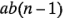grados de libertad para el error. Observe que la suma del número de grados de libertad en el lado derecho de la ecuación 5-5 es igual al número total de grados de libertad.

Cada suma de cuadrados dividida por sus grados de libertad es un cuadrado medio. Los valores esperados de los cuadrados medios son: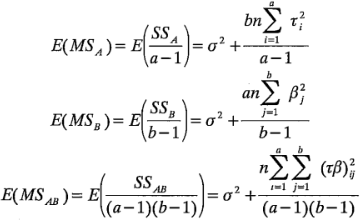

y


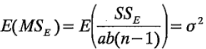
Observe que, si es verdadera la hipótesis nula de que no hay efectos de los tratamientos de los renglones, ni de los tratamientos de las columnas, ni interacción, entonces 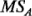, , 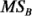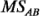y 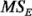 son todas estimaciones de 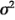. Sin embargo, si hay diferencias entre los efectos de los tratamientos de los renglones, por ejemplo, entonces  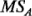será mayor que 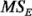. De manera similar, si están presentes efectos de los tratamientos de las columnas o de la interacción, entonces los cuadrados medios correspondientes serán mayores que 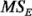. Por lo tanto, para probar la significación de los dos efectos principales y su interacción, simplemente se divide el cuadrado medio correspondiente por el cuadrado medio del error. Los valores grandes de este cociente implican que los datos no apoyan la hipótesis nula.

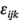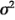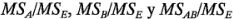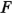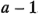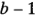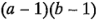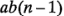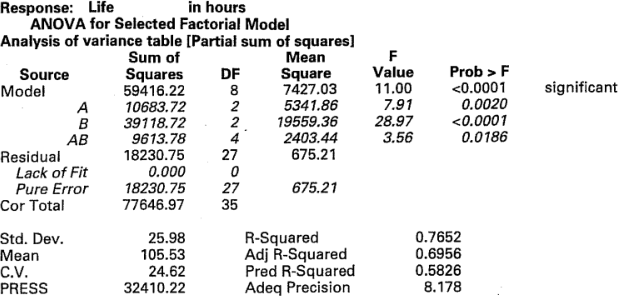
Si se supone que el modelo (ecuación 5-1) es adecuado y que los términos del error  tienen una distribución normal e independiente con varianza  constante, entonces cada uno de los cocientes de cuadrados medios  se distribuyen como  con , y  grados de libertad en el numerador, respectivamente, y  grados de libertad en el denominador, y la región crítica sería la cola superior de la distribución 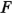. El procedimiento de prueba suele resumirse en una tabla del análisis de varianza, como se muestra en la tabla 5-3.


En lo que a los cálculos se refiere, por lo general se emplea un paquete de software de estadística para realizar el análisis de varianza. Sin embargo, no es complicado obtener fórmulas para calcular manualmente las sumas de cuadrados de la ecuación 5-5. La suma de cuadrados total se calcula como de costumbre con: 


Las sumas de cuadrados de los efectos principales son:

y


Es conveniente obtener 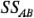 en dos pasos. Se calcula primero la suma de cuadrados entre los totales de las  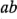celdas, a la que se denomina la suma de cuadrados debida a los "subtotales": 


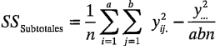
Esta suma de cuadrados también contiene a 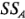 y 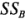. Por 10 tanto, el segundo paso consiste en calcular  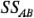como:

Puede calcularse 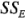 por sustracción como:

ó


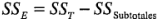
Comparaciones múltiples

Cuando el análisis de varianza indica que las medias de los renglones o las columnas difieren, por lo general es de interés hacer comparaciones entre las medias individuales de los renglones o las columnas para descubrir diferencias específicas. Los métodos de comparaciones múltiples revisados en el capítulo 3 son útiles a este respecto.

Se ilustra ahora el uso de la prueba de Tukey con los datos de la vida de la batería del ejemplo 5-l. Observe que, en este experimento, la interacción es significativa. Cuando la interacción es significativa, las comparaciones entre las medias de uno de los factores (por ejemplo, 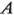) pueden ser oscurecidas por la interacción 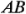. Una forma de abordar esta cuestión consiste en fijar el factor  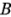en un nivel específico y aplicar la prueba de Tukey a las medias del factor  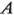con ese nivel. Para ilustrar, suponga que en el ejemplo 5-l el interés se encuentra en detectar las diferencias entre las medias de los tres tipos de material. Puesto que la interacción es significativa, esta comparación se hace con un solo nivel de la temperatura, por ejemplo, el nivel 2 (70°F). Se supone que la mejor estimación de la varianza del error es  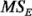de la tabla del análisis de varianza, utilizando el supuesto de que la varianza del error experimental es la misma para todas las combinaciones de tratamientos.


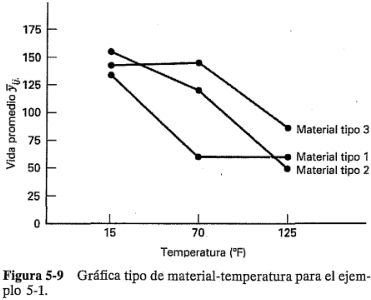
Los promedios de los tres tipos de material a 70°F dispuestos en orden ascendente son:


y


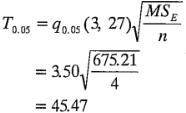
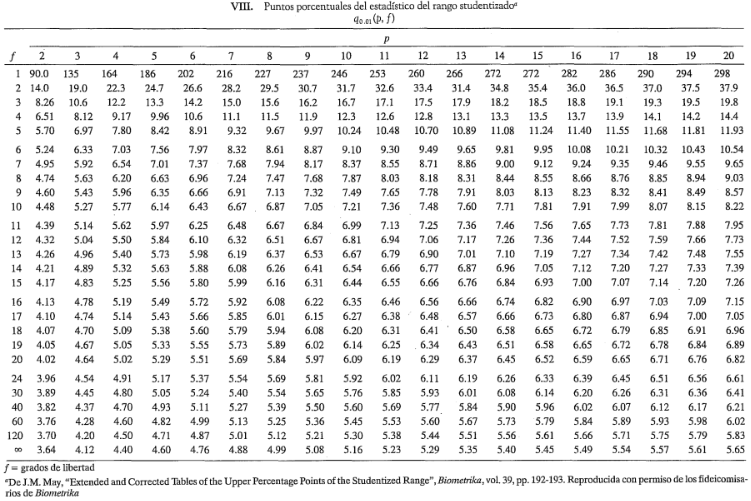
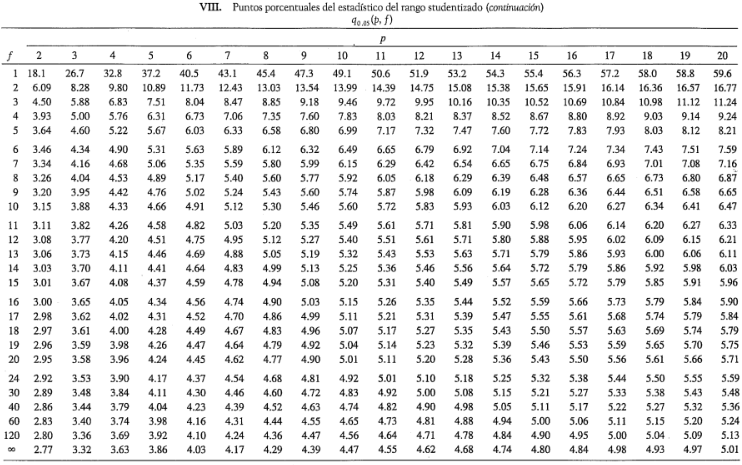
donde 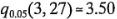 se obtiene por interpolación en la tabla VIII del apéndice. Las comparaciones por pares dan como resultado:


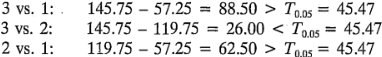
Este análisis indica que, con el nivel de temperatura de 70°F, la vida media de la batería es la misma para los materiales tipos 2 y 3, y que la vida media de la batería para el material tipo 1 es significativamente menor.

Si la interacción es significativa, el experimentador podría comparar las medias de todas las 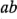 celdas para determinar cuáles difieren significativamente. En este análisis, las diferencias entre las medias de las celdas incluyen los efectos de la interacción, así como ambos efectos principales. En el ejemplo 5-1, esto daría 36 comparaciones entre todos los pares posibles de las nueve medias de las celdas.

Salida de computadora

En la figura 5-10 se presenta la salida de computadora de Design-Expert para los datos de la vida de la batería del ejemplo 5-1. Observe que:


y que


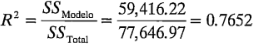
Es decir, cerca de 77% de la variabilidad de la vida de la batería es explicada por el material de la placa de la batería, la temperatura y la interacción entre el tipo de material y la temperatura. En la salida de computadora se muestran también los residuales del modelo ajustado. A continuación, se indica cómo usar estos residuales para verificar la adecuación del modelo.




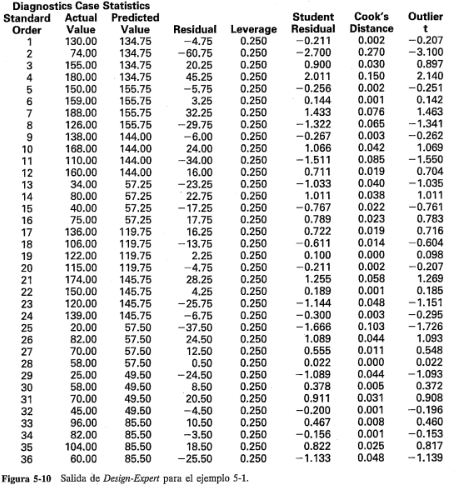
APENDICE (Tabla VIII)



Última modificación: viernes, 16 de febrero de 2024, 13:14