5.6.- Formación de bloques en un diseño factorial

Se han revisado los diseños factoriales en el contexto de un experimento completamente aleatorizado. En ocasiones no es factible o práctico hacer la aleatorización completa de todas las corridas de un diseño factorial. Por ejemplo, la presencia de un factor perturbador puede hacer necesario que el experimento se corra en bloques. Los conceptos básicos de la formación de bloques se analizaron en el capítulo 4 en el contexto de un experimento con un solo factor. Ahora se indica la forma en que la formación de bloques puede incorporarse en un diseño factorial. Otros aspectos de la formación de bloques en diseños factoriales se presentan en los capítulos 7, 8, 9 y 13.

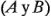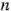Considere un experimento factorial con dos factores  y  replicas. El modelo estadístico lineal de este diseño es:

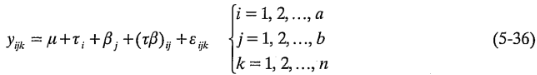
donde 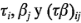 representan los efectos de los factores 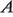,  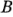y la interacción 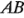, respectivamente. Suponga ahora que para realizar este experimento se necesita una materia prima particular. Esta materia prima está disponible en lotes cuyo tamaño no es suficiente para permitir que se corran todas las 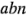combinaciones de los tratamientos con el mismo lote. Sin embargo, si un lote contiene material suficiente para hacer  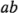observaciones, entonces un diseño alternativo es correr cada una de las 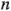réplicas utilizando un lote separado de materia prima. Por consiguiente, los lotes de materia prima representan una restricción sobre la aleatorización o un bloque, y se corre una sola réplica de un experimento factorial completo dentro de cada bloque. El modelo de los efectos para este nuevo diseño es: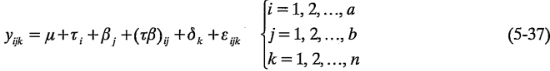

donde 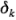 es el efecto del bloque k-ésimo. Desde luego, dentro de un bloque el orden en que se corren las combinaciones de los tratamientos está completamente aleatorizado.

En el modelo (ecuación 5-37) se supone que la interacción entre los bloques y los tratamientos es insignificante. Anteriormente se estableció el mismo supuesto en el análisis de diseños de bloques aleatorizados. Si estas interacciones existen, no pueden separarse del componente del error. De hecho, el término del error en este modelo se compone en realidad de las interacciones 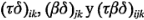. En la tabla 5-18 se describe el análisis de varianza. La disposición tiene un gran parecido con la de un diseño factorial, con la suma de cuadrados del error reducida por la suma de cuadrados de los bloques. En lo que a los cálculos se refiere, la suma de cuadrados de los bloques se encuentra como la suma de cuadrados entre los totales de los 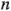bloques .

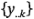En el ejemplo anterior, la aleatorización se restringió al interior de un lote de materia prima. En la práctica, una diversidad de fenómenos pueden producir restricciones sobre la aleatorización, como el tiempo, los operadores, etc. Por ejemplo, si el experimento factorial completo no pudo correrse en un día, entonces el experimentador podría correr una réplica completa el día 1, una segunda réplica el día 2, etc. Por consiguiente, cada día sería un bloque.

En el caso de dos restricciones sobre la aleatorización, cada una con 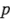 niveles, si el número de combinaciones de los tratamientos en un diseño factorial de  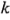factores es exactamente igual al número de niveles de la restricción, es decir, si 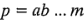, entonces el diseño factorial puede correrse en un cuadrado latino 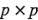. Por ejemplo, considere una modificación del experimento de la detección del objetivo en el

radar del ejemplo 5-6. Los factores de este experimento son el tipo de filtro (dos niveles) y el desorden de

terreno (tres niveles), y los operadores se consideran como bloques. Suponga ahora que debido a limitaciones de tiempo, sólo pueden hacerse seis corridas por día. Por lo tanto, los días se convierten en una segunda restricción sobre la aleatorización, lo cual resulta en un diseño del cuadrado latino 6 x 6, como se muestra en la tabla 5-21. En esta tabla se han usado las letras minúsculas 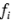 y 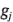 para representarlos niveles i-ésimo y j-ésimo del tipo de filtro y del desorden de terreno, respectivamente. Es decir, 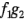representa el filtro tipo 1 y un desorden de terreno intermedio. Observe que se necesitan ahora seis operadores, en lugar de los cuatro del experimento original, por lo que el número de combinaciones de tratamientos en el diseño factorial 3 x 2 es exactamente igual al número de niveles de restricción. Además, en este diseño cada operador se usaría una sola vez en cada día. Las letras latinas A, B, C, D, E y F representan las 3 x 2 =6 combinaciones de tratamientos del diseño factorial como sigue: .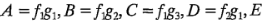

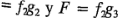Los cinco grados de libertad entre las seis letras latinas corresponden a los efectos principales del tipo de filtro (un grado de libertad), el desorden de terreno (dos grados de libertad) y su interacción (dos grados de libertad). El modelo estadístico lineal de este diseño es:

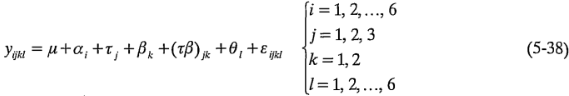
donde 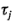 y 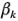 son los efectos del desorden de terreno y del tipo de filtro, respectivamente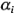, y  y 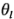 representan las restricciones sobre la aleatorización de los días y los operadores, respectivamente. Para calcular las sumas de cuadrados, la siguiente tabla de dos vías de los totales de los tratamientos es útil:

Además, los totales de los renglones y las columnas son: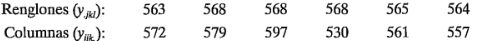

En la tabla 5-22 se resume el análisis de varianza. Se ha agregado una columna a esta tabla que indica cómo se determina el número de grados de libertad de cada suma de cuadrados.