6.2.- El diseño 2^2

El primer diseño de la serie 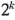 es el que sólo tiene dos factores, por ejemplo,  y ; cada uno se corre a dos niveles. A este diseño se le llama diseño factorial 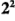. Los niveles de los factores pueden denominarse arbitrariamente "bajo" y "alto". Como un ejemplo, considere la investigación del efecto de la concentración del reactivo y de la cantidad del catalizador sobre la conversión (rendimiento) de un proceso químico. Sea la concentración del reactivo el factor , y sean 15 y 25 por ciento los dos niveles de interés. El catalizador es el factor , con el nivel alto denotando el uso de 2 libras del catalizador y el nivel bajo denotando el uso de 1 libra. Se hacen tres réplicas del experimento, y los datos son los siguientes:

Las combinaciones de los tratamientos se ilustran gráficamente en la figura 6-1. Por convención, el efecto de un factor se denota con una letra mayúscula latina. Por 10 tanto, "" se refiere al efecto del factor , "" al efecto del factor , y "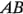" a la interacción 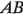. En el diseño 22, los niveles bajo y alto de y  se denotan por "-" y "+", respectivamente, en los ejes  y . Por lo tanto, - en el eje  representa el nivel bajo de la concentración (15%), mientras que + representa el nivel alto (25%), Y- en el eje representa el nivel bajo del catalizador, mientras que + denota el nivel alto.

Las cuatro combinaciones de tratamientos suelen representarse con letras minúsculas, como se muestra en la figura 6-1. Por la figura se observa que el nivel alto de cualquiera de los factores en una combinación de tratamientos se denota por la letra minúscula correspondiente y que el nivel bajo de un factor. En una combinación de tratamientos se denota por la ausencia de la letra respectiva. Por lo tanto, 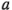representa la combinación de tratamientos con  en el nivel alto y en el nivel bajo, 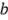representa  en el nivel bajo y en el nivel alto, y 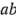representa ambos factores en el nivel alto. Por convención, se usa (1) para denotar que ambos factores están en el nivel bajo. Esta notación se utiliza en todas las series .

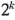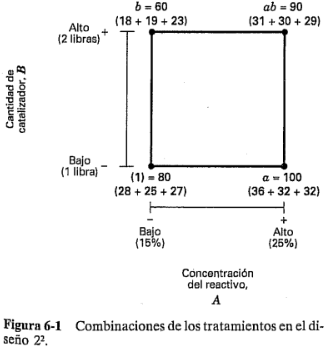
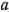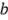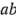En un diseño factorial con dos niveles, el efecto promedio de un factor puede definirse como el cambio en la respuesta producido por un cambio en el nivel de ese factor promediado para los niveles del otro factor. Asimismo, los símbolos (1),,  y  representan ahora el total de las 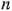réplicas hechas con la combinación de los tratamientos, como se ilustra en la figura 6-1. Ahora el efecto de  en el nivel bajo de  es 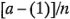 y el efecto de  con el nivel alto de  es 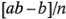. Al promediarse estas dos cantidades se obtiene el efecto principal de :

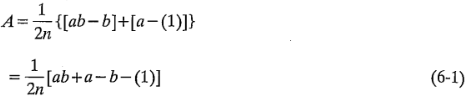
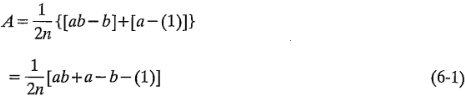
El efecto principal promedio de se encuentra a partir del efecto de  con el nivel bajo de  (es decir, 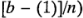 y con el alto de  (o sea, 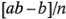) como: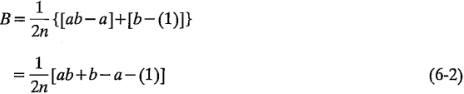

El efecto de la interacción 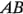 se define como la diferencia promedio entre el efecto de  con el nivel alto de y el efecto de con el nivel bajo de . Por lo tanto,

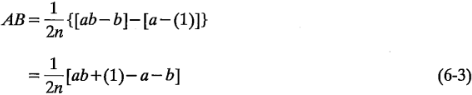
De manera alternativa, 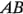puede definirse como la diferencia promedio entre el efecto de con el nivel alto de y el efecto de con el nivel bajo de . Esto llevará también a la ecuación 6-3. Las fórmulas de los efectos de , y 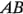pueden deducirse con otro método. El efecto de  puede encontrarse como la diferencia en la respuesta promedio de las dos combinaciones de tratamientos situadas a la derecha del cuadrado de la figura 6-1 (a este promedio se le llama 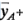, porque es la respuesta promedio con las combinaciones de tratamientos donde está en el nivel alto) y las dos combinaciones de tratamientos situadas a la izquierda del cuadrado de la figura 6-1 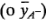. Es decir, 

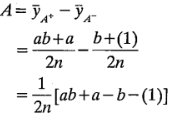
Se trata exactamente del mismo resultado que el de la ecuación 6-1. El efecto de , ecuación 6-2, se encuentra como la diferencia entre el promedio de las dos combinaciones de tratamientos de la parte superior del cuadrado 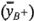 y el promedio de las dos combinaciones de tratamientos de la parte inferior 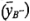, o 

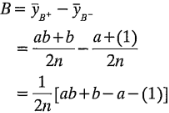
Por último, el efecto de la interacción 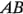es el promedio de las combinaciones de tratamientos de la diagonal de derecha a izquierda del cuadrado  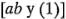menos el promedio de las combinaciones de tratamientos de la diagonal de izquierda a derecha 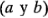, o 

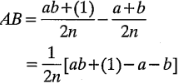
resultado que es idéntico a la ecuación 6-3.

Utilizando el experimento de la figura 6-1, los efectos promedio pueden estimarse como:

El efecto de (concentración del reactivo) es positivo; esto sugiere que al incrementar  del nivel bajo (15%) al nivel alto (25%), el rendimiento se incrementará. El efecto de (catalizador) es negativo; esto sugiere que al incrementar la cantidad del catalizador que se agrega al proceso se reducirá el rendimiento. El efecto de la interacción parece ser pequeño en comparación con los dos efectos principales.

En muchos experimentos que incluyen diseños 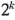, se examinará la magnitud y la dirección de los efectos de los factores a fin de determinar las variables que son de posible importancia. En la mayoría de los casos puede usarse el análisis de varianza para confirmar esta interpretación. Hay varios paquetes de software de estadística excelentes que son útiles para establecer y analizar diseños 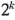. Se cuenta también con métodos especiales que ahorran tiempo cuando los cálculos se hacen manualmente.

Considere las sumas de cuadrados de , y 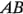. Observe, por la ecuación 6-1, que se usó un contraste para estimar , a saber:

A este contraste suele l1amársele el efecto total de . A partir de las ecuaciones 6-2 y 6-3, se observa que también se usan contrastes para estimar y 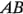. Además, estos tres contrastes son ortogonales. La suma de cuadrados de cualquier contraste puede calcularse con la ecuación 3-29, la cual establece que la suma de cuadrados del contraste es igual al cuadrado del contraste dividido por el número de observaciones en cada total del contraste multiplicado por la suma de cuadrados de los coeficientes del contraste. Por consiguiente, se tienen:

y

como las sumas de cuadrados de , y .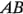

Al utilizar el experimento de la figura 6-1, las sumas de cuadrados de las ecuaciones 6-5, 6-6 y 6-7 pueden encontrarse como:

y

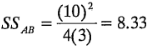
La suma de cuadrados total se encuentra como de costumbre, es decir:

En general, 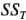 tiene 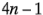 grados de libertad. La suma de cuadrados del error, con  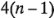grados de libertad, suele calcularse por sustracción como:

Para el experimento de la figura 6-1, se obtiene: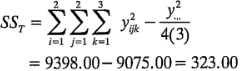

y

al utilizar 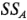, 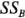y 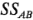de la ecuación 6-8. En la tabla 6-1 se resume el análisis de varianza completo. Con base en los valores 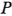, se concluye que los efectos principales son estadísticamente significativos y que no hay interacción entre estos factores. Esto confirma la interpretación de los datos que se hizo originalmente con base en las magnitudes de los efectos de los factores.

Con frecuencia resulta conveniente escribir las combinaciones de los tratamientos en el orden (1), 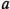, , 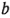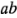. Se hace referencia a esto como el orden estándar (u orden de Yates, por el Dr. Frank Yates). Al utilizar este orden estándar, se observa que los coeficientes de los contrastes usados para estimar los efectos son: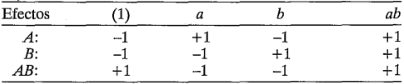

Observe que los coeficientes de los contrastes para estimar el efecto de la interacción son sólo el producto de los coeficientes correspondientes de los dos efectos principales. El coeficiente de un contraste es siempre +1 o -1, y puede usarse una tabla de signos positivos y negativos como la tabla 6-2 para determinar el signo correcto para cada combinación de tratamientos. Los encabezados de las columnas de la tabla 6-2 son los efectos principales ( y ), la interacción e I, que representa el total o promedio del experimento completo. Observe que la columna que corresponde a J incluye únicamente signos positivos. Las etiquetas de los renglones son las combinaciones de los tratamientos. Para encontrar el contraste para estimar cualquier efecto, simplemente se multiplican los signos de la columna apropiada de la tabla por la combinación de tratamientos correspondiente y se hace la suma. Por ejemplo, para estimar , el contraste es -(1) + - + 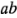, que concuerda con la ecuación 6-1.

El modelo de regresión

En un diseño factorial 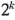 es sencillo expresar los resultados del experimento en términos de un modelo de regresión. Puesto que 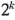es tan sólo un diseño factorial, podría usarse un modelo de los efectos o de las medias, pero el enfoque del modelo de regresión es mucho más natural e intuitivo. Para el experimento del proceso químico de la figura 6-1, el modelo de regresión es: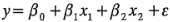

donde 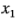es una variable codificada que representa la concentración del reactivo y 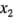es una variable codificada que representa la cantidad del catalizador y las  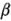son los coeficientes de regresión. La relación entre las variables naturales -la concentración del reactivo y la cantidad de catalizador- y las variables codificadas es:

y

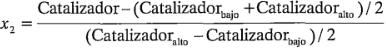
Cuando las variables naturales sólo tienen dos niveles, esta codificación producirá la familiar notación 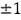 para los niveles de las variables codificadas. Para ilustrar esto en el ejemplo tratado, observe que:

Por lo tanto, si la concentración está en el nivel alto (Concentración = 25%), entonces 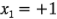; si la concentración está en el nivel bajo (Concentración = 15%), entonces 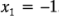. Además, 

Por lo tanto, si el catalizador está en el nivel alto (Catalizador = 2 libras), entonces 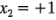; si el catalizador está en el nivel bajo (Catalizador = 1 libra), entonces .

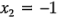El modelo de regresión ajustado es: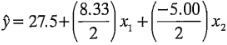

donde la ordenada al origen es el gran promedio de las 12 observaciones, y los coeficientes de regresión 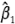 y 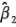 son la mitad de las estimaciones de los efectos de los factores correspondientes. La razón de que el coeficiente de regresión sea la mitad de la estimación del efecto es que un coeficiente de regresión mide el efecto de un cambio unitario en  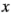y sobre la media de 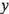, y la estimación del efecto se basa en un cambio de dos unidades (de -1 a + 1). Se demostrará más adelante que este método simple para estimar los coeficientes de regresión consiste en producir las estimaciones de mínimos cuadrados de los parámetros. Ver también el material suplementario de este capítulo.

Residuales y adecuación del modelo

El modelo de regresión puede usarse para obtener el valor predicho o ajustado de y en los cuatro puntos del diseño. Los residuales son las diferencias entre el valor observado y el valor ajustado de y. Por ejemplo, cuando la concentración del reactivo está en el nivel bajo 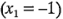y el catalizador está en el nivel bajo 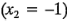, el rendimiento predicho es:

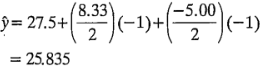
Hay tres observaciones en esta combinación de tratamientos, y los residuales son:

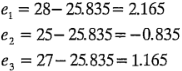
Los valores predichos y los residuales restantes se calculan de manera similar. Para el nivel alto de la concentración del reactivo y el nivel bajo del catalizador,

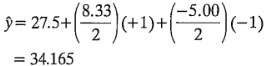
y

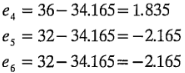
Para el nivel bajo de la concentración del reactivo y el nivel alto del catalizador,

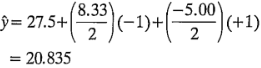
y

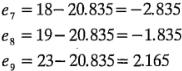
Por último, para el nivel alto de ambos factores,

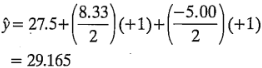
y

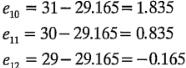
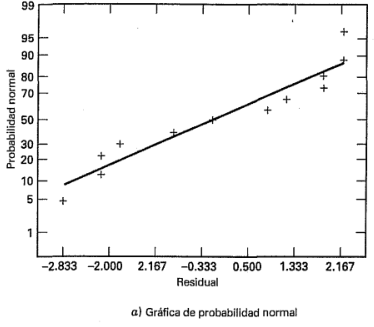
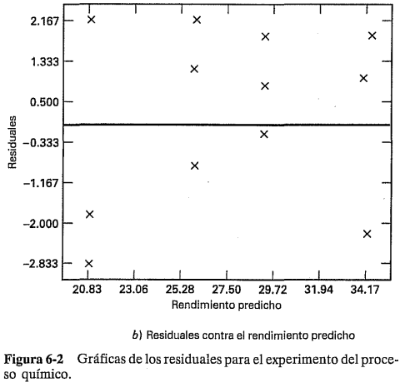
En la figura 6-2 se presenta una gráfica de probabilidad normal de estos residuales y una gráfica de los residuales contra el rendimiento predicho. Estas gráficas parecen ser satisfactorias, por lo que no hay razón para sospechar problemas con la validez de las conclusiones.

La superficie de respuesta

El modelo de regresión

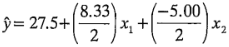
puede usarse para generar gráficas de superficie de respuesta. Si se desea construir estas gráficas en términos de los niveles de los factores naturales, entonces simplemente las relaciones entre las variables naturales y las codificadas que se dieron anteriormente se sustituyen en el modelo de regresión, de donde se obtiene: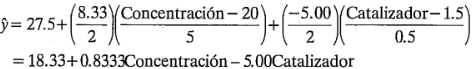

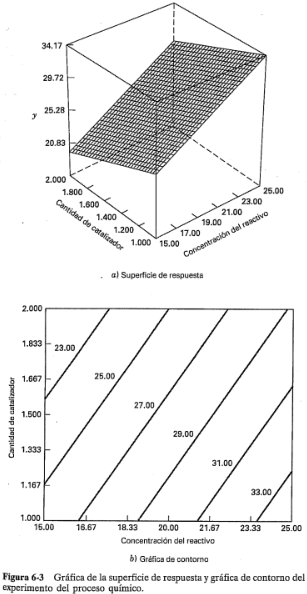
En la figura 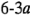 se presenta la gráfica de superficie de respuesta tridimensional del rendimiento de este modelo, y la figura  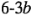es la gráfica de contorno. Puesto que el modelo es de primer orden (es decir, contiene únicamente los efectos principales), la superficie de respuesta ajustada es un plano. Al examinar la gráfica de contorno se observa que el rendimiento aumenta cuando la concentración del reactivo se incrementa y la cantidad de catalizador disminuye. Frecuentemente se usa una superficie ajustada como ésta para encontrar la dirección del mejoramiento potencial de un proceso. Una manera formal de hacer esto, llamada método del ascenso más pronunciado, se presentará en el capítulo 11 cuando se estudien los métodos para realizar la exploración sistemática de las superficies de respuesta.