6.5.- Una sola réplica del diseño 2^k

Incluso para un número moderado de factores, el número total de combinaciones de tratamientos en un diseño factorial 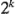es grande. Por ejemplo, un diseño 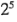tiene 32 combinaciones de tratamientos, un diseño 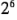tiene 64 combinaciones de tratamientos, etc. Debido a que por lo general los recursos son limitados, el número de réplicas que el experimentador puede emplear quizás esté restringido. Con frecuencia, los recursos disponibles permiten hacer únicamente una sola réplica del diseño, a menos que el experimentador esté dispuesto a omitir algunos de los factores originales.

Un riesgo obvio cuando se realiza un experimento que tiene una sola corrida para cada combinación de prueba es que el modelo puede ajustarse al ruido. Es decir, si la respuesta y es sumamente variable, pueden resultar conclusiones engañosas del experimento. La situación se ilustra en la figura 6-9a. En esta figura, la línea recta representa el verdadero efecto del factor. Sin embargo, debido a la variabilidad aleatoria presente en la variable de respuesta (representada por la franja sombreada), el experimentador obtiene en realidad las dos respuestas medidas representadas por los puntos negros. Por consiguiente, el efecto del factor estimado está cerca de cero y el experimentador ha llegado a una conclusión errónea respecto de este factor. Ahora bien, si hay menos variabilidad en la respuesta, la posibilidad de una conclusión errónea será más reducida. Otra forma de asegurarse de que se obtienen estimaciones confiables de los efectos es incrementando la distancia entre los niveles bajo (-) y alto (+) del factor, como se ilustra en la figura 6-9b. Observe que en esta figura la distancia incrementada entre los niveles bajo y alto del factor resulta en una estimación razonable del verdadero efecto del factor.

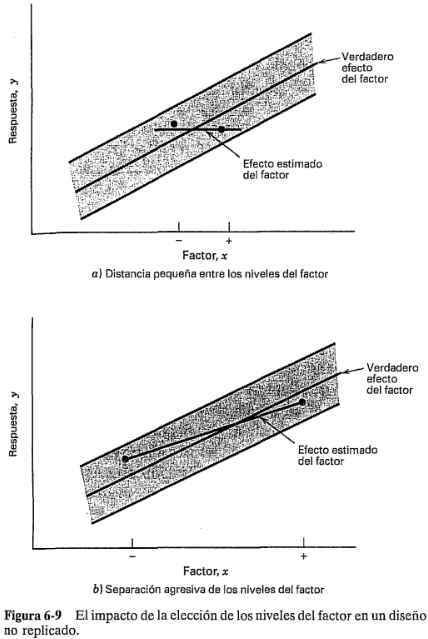
El uso de la estrategia de una sola réplica es común en los experimentos de exploración cuando hay un número relativamente grande de factores bajo consideración. Debido a que en estos casos nunca puede tenerse la certeza absoluta de que el error experimental es pequeño, una buena práctica en este tipo de experimentos es separar los niveles de los factores de manera agresiva. Quizás el lector encuentre útil releer las pautas generales para elegir los niveles de los factores del capítulo 1.

Una sola réplica de un diseño 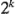se denomina en ocasiones diseño factorial no replicado. Con una sola réplica, no se cuenta con ninguna estimación interna del error (o "error puro"). Una forma de abordar este análisis de un diseño factorial no replicado consiste en suponer que algunas interacciones de orden superior son insignificantes y combinar sus cuadrados medios para estimar el error. Esto es una apelación al principio de efectos esparcidos; es decir, la mayoría de los sistemas están dominados por algunos de los efectos principales y las interacciones de orden inferior, y la mayor parte de las interacciones de orden superior son insignificantes.

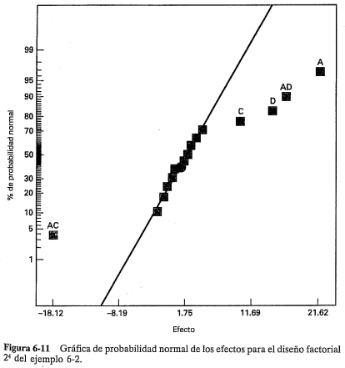
Cuando se analizan datos de diseños factoriales no replicados, ocasionalmente ocurren interacciones de orden superior reales. El uso de un cuadrado medio del error que se obtiene agrupando las interacciones de orden superior no es apropiado en estos casos. Un método de análisis atribuido a Daniel [35a] proporciona una forma simple de resolver este problema. Daniel sugiere examinar una gráfica de probabilidad normal de las estimaciones de los efectos. Los efectos que son insignificantes siguen una distribución normal, con media cero y varianza 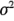, y tenderán a localizarse sobre una línea recta en esta gráfica, mientras que los efectos significativos tendrán medias diferentes de cero y no se localizarán sobre la línea recta. Por lo tanto, el modelo preliminar se especificará de tal modo que contenga aquellos efectos que aparentemente son diferentes de cero, con base en la gráfica de probabilidad normal. Los efectos aparentemente insignificantes se combinan como una estimación del error.

Proyección de un diseño

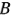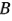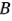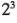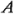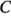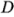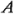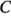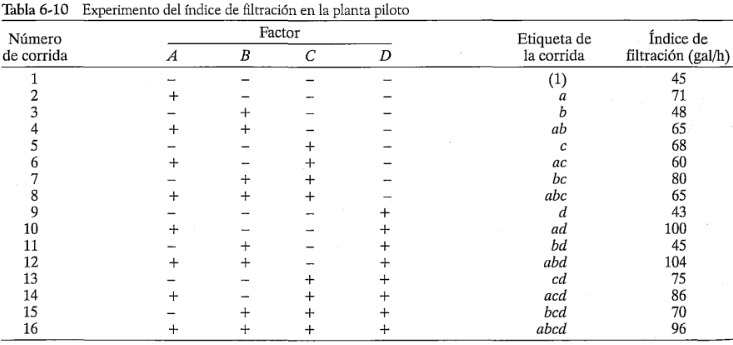
Es posible hacer otra interpretación de los efectos de la figura 6-11. Puesto que (presión) no es significativa y todas las interacciones en las que interviene  son insignificantes, puede descartarse del experimento, de tal modo que el diseño se convierte en un factorial en ,  y  con dos réplicas. Esto es fácil de ver examinando únicamente las columnas , y 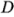 en la matriz del diseño que se muestra en la tabla 6-10 y observando que esas columnas forman dos réplicas de un diseño  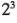En la tabla 6-13 se resume el análisis de varianza de los datos utilizando este supuesto de simplificación. Las conclusiones que se sacarían de este análisis se mantienen en esencia sin cambios respecto de las del ejemplo 6-2. 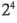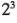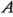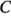Observe que al hacer la proyección de la réplica única del diseño en un diseño con dos réplicas, se tiene ahora tanto una estimación de la interacción 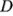como una estimación del error basada en lo que en ocasiones se denomina réplica oculta.

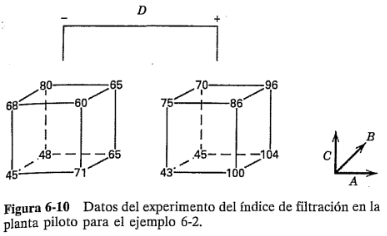
El concepto de proyectar un diseño factorial no replicado en un diseño factorial con réplicas en menos factores es muy útil. En general, si se tiene una sola réplica del diseño 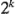y si 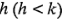factores son insignificantes y pueden descartarse, entonces los datos originales corresponden a un diseño factorial completo con dos niveles en los factores restantes con 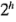réplicas.

Verificación de diagnóstico

Deberán aplicarse las verificaciones de diagnóstico usuales a los residuales de un diseño 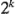. El análisis realizado indica que los únicos efectos significativos son 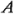= 21.625, 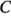= 9.875, 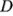= 14.625,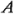 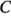=-18.125 y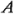 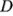 = 16.625. Si esto es correcto, los índices de filtración estimados están dados por: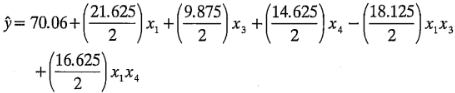

donde 70.06 es la respuesta promedio y las variables codificadas 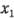, , 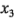 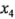asumen valores entre -1 y + 1. El índice de filtración predicho para la corrida (1) es: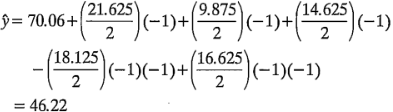

Puesto que el valor observado es 45, el residual es 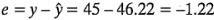. A continuación, se presentan los valores de 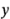,  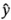y 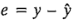 para las 16 observaciones.

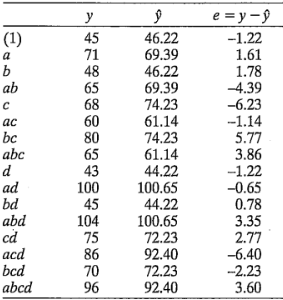
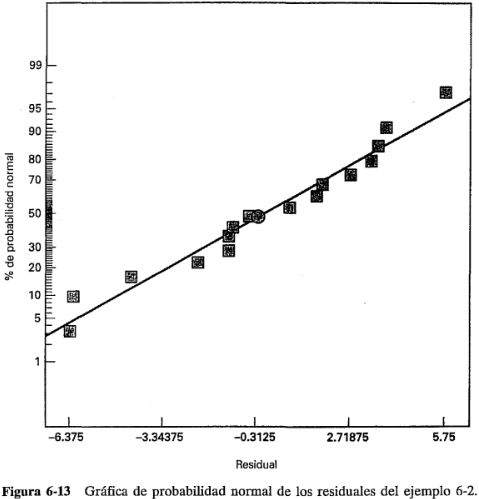
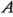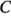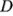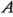
En la figura 6-13 se muestra la gráfica de probabilidad normal de los residuales. Los puntos de esta gráfica se localizan razonablemente próximos a una línea recta, brindando apoyo a la conclusión de que , , ,  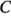y 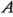 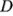son los únicos efectos significativos y que se satisfacen los supuestos fundamentales del análisis.

La superficie de respuesta

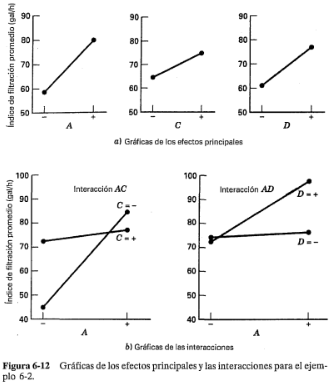
Las gráficas de las interacciones de la figura 6-12 se utilizaron para ofrecer una interpretación práctica de los resultados de este experimento. En ocasiones es útil emplear la superficie de respuesta para este fin.

La superficie de respuesta se genera por el modelo de regresión: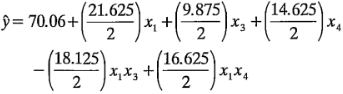

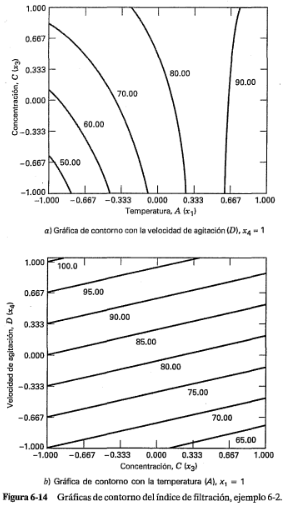
En la figura 6-14a se muestra la gráfica de contorno de la superficie de respuesta cuando la velocidad de agitación está en el nivel alto (es decir, 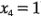). Los contornos se generan a partir del modelo anterior con 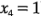, ó:

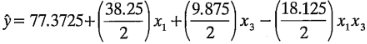
Observe que los contornos son líneas curvas porque el modelo contiene un término de interacción. La figura 6-14b es la gráfica de contorno de la superficie de respuesta cuando la temperatura está en el nivel alto (es decir, 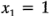). Cuando se hace 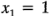en el modelo de regresión se obtiene: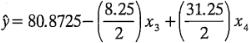

Estos contornos son rectas paralelas porque el modelo contiene únicamente los efectos principales de los factores 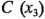 y .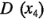

Ambas gráficas de contorno indican que, si se quiere maximizar el índice de filtración, las variables 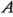 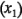y 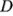 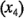deberán estar en el nivel alto y que el proceso es relativamente robusto para la concentración 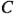. Se obtuvieron conclusiones similares a partir de las gráficas de las interacciones.

La mitad de gráfica normal de los efectos

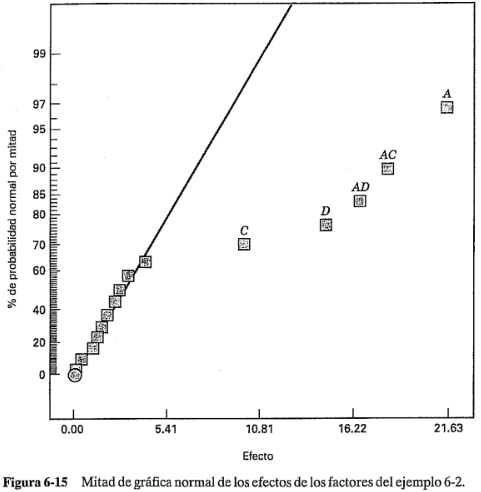
Una alternativa para la gráfica de probabilidad normal de los efectos de los factores es la mitad de gráfica normal. Es una gráfica del valor absoluto de las estimaciones de los efectos contra sus probabilidades normales acumuladas. En la figura 6-15 se muestra la mitad de gráfica normal de los efectos para el ejemplo 6-2. La línea recta de la mitad de gráfica normal siempre pasa por el origen y deberá pasar también cerca del valor de los datos del percentil cincuenta. Muchos analistas sienten que es más fácil interpretar la mitad de gráfica normal, en particular si sólo se cuenta con pocas estimaciones de los efectos, como cuando el experimentador ha usado un diseño de ocho corridas. Algunos paquetes de software construirán ambas graficas.

Otros métodos para analizar diseños factoriales no replicados

El procedimiento de análisis estándar para un diseño factorial de dos factores no replicado es la gráfica normal (O mitad de gráfica normal) de los efectos estimados de los factores. Sin embargo, los diseños no replicados son tan usados en la práctica que se han propuesto muchos procedimientos formales de análisis para resolver la subjetividad de la gráfica de probabilidad normal. Hamada y Balakrishnan [52] compararon algunos de estos métodos. Encontraron que el método propuesto por Lenth [70] tiene una potencia adecuada para detectar efectos significativos. También es fácil de implementar y, como resultado, está empezando a aparecer en algunos paquetes de software para analizar datos de diseños factoriales no replicados. Se ofrece una breve descripción del método de Lenth.

Suponga que se tienen 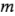 contrastes de interés, por ejemplo 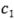, , 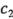..., 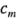. Si el diseño es un factorial  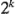no replicado, estos contrastes corresponden a las  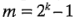estimaciones de los efectos de los factores. La base del método de Lenth es estimar la varianza de un contraste a partir de las estimaciones más pequeñas (en valor absoluto) de los contrastes. Sean:

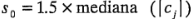
y

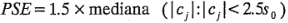
PSE denota el "pseudo error estándar", y Lenth demuestra que es un estimador razonable de la varianza del contraste cuando no hay muchos efectos activos (significativos). El PSE se usa para juzgarla significación de los contrastes. Un contraste individual puede compararse con el margen de error (ME, margin of error).

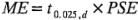
donde los grados de libertad se definen como 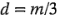. Para hacer inferencias sobre un grupo de contrastes, Lenth sugiere usar el margen de error simultáneo (SME, simultaneous margin of error).

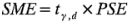
donde el punto porcentual de la distribución t que se usa es 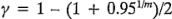0.

Para ilustrar el método de Lenth, considere el experimento 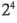del ejemplo 6-2. Los cálculos dan como resultado 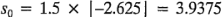y 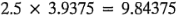, de donde: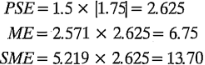

Considere ahora las estimaciones de los efectos de la tabla 6-12. El criterio 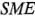indicaría que los cuatro efectos más grandes (en magnitud) son significativos, ya que las estimaciones de sus efectos exceden 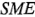. El efecto principal de 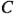es significativo de acuerdo con el criterio 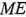, pero no con respecto al 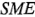. Sin embargo, puesto que es evidente que la interacción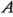 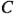es importante, probablemente 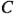se incluiría en la lista de efectos significativos. Observe que en este ejemplo el método de Lenth produjo la misma respuesta que la obtenida anteriormente con el examen de la gráfica de probabilidad normal de los efectos.

Varios autores (ver Ramada y Balakrishnan [52], Loughin [73], Loughin y Noble [74] y Larntz y Whitcomb [69]) han hecho notar que el método de Lenth falla para controlar los índices del error tipo I, y que pueden usarse métodos de simulación para calibrar su procedimiento. Larntz y Whitcomb [69] sugieren reemplazar los multiplicadores 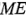y 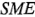con multiplicadores ajustados de la siguiente manera:

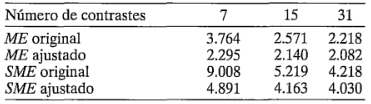
Estos resultados coinciden en gran medida con los de Ye y Ramada [114]. En general, el método de Lenth es un procedimiento ingenioso y útil. Sin embargo, recomendamos utilizarlo como complemento de la gráfica de probabilidad normal usual de los efectos, no como su sustituto.

Bisgaard [10] ha proporcionado una sutil técnica gráfica, llamada carta de inferencia condicional, como ayuda para interpretar la gráfica de probabilidad normal. La finalidad de esta gráfica es ayudar al experimentador a juzgar los efectos significativos. Esto sería relativamente sencillo si se conociera la desviación estándar 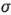, o si pudiera estimarse a partir de los datos. En diseños no replicados, no se cuenta con ninguna estimación interna de 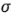, por lo que la carta de inferencia condicional está diseñada para ayudar al experimentador a evaluarla magnitud de los efectos para un rango de valores de la desviación estándar.

Bisgaard fundamenta la gráfica en el resultado de que el error estándar de un efecto, en un diseño de dos niveles con N corridas (para un diseño factorial no replicado, 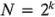), es:

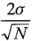
donde 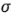es la desviación estándar de una observación individual. Entonces ±2 veces el error estándar de un efecto es: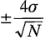

Una vez que se estiman los efectos, se hace una gráfica como la que se muestra en la figura 6-16, con las estimaciones de los efectos graficadas en el eje vertical, o eje y. En esta figura se han usado las estimaciones de los efectos del ejemplo 6-2. El eje horizontal, o 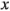, de la figura 6-16 es la escala de la desviación estándar (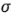). Las dos rectas están en: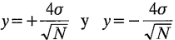

En el ejemplo tratado aquí, 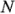=16, por lo que las rectas están en  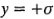y 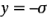. Por lo tanto, para cualquier valor dado de la desviación estándar a, la distancia entre estas dos rectas puede leerse como un intervalo de confianza de 95% aproximado para los efectos insignificantes.

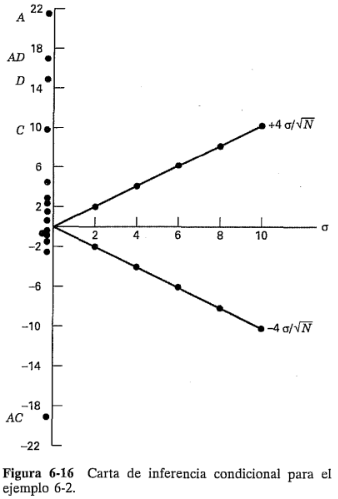
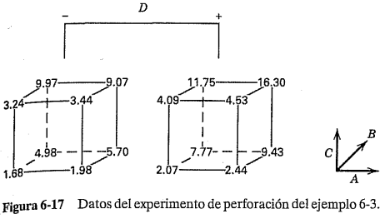
En la figura 6-16 se observa que, si el experimentador piensa que la desviación estándar está entre 4y 8, entonces los factores 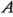, , 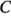 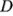y las interacciones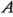 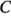y 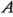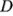son significativos. Si el experimentador piensa que la desviación estándar tiene un valor de hasta 10, el factor 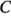quizá no sea significativo. Es decir, para cualquier supuesto dado acerca de la magnitud de a, el experimentador puede construir una "cinta de medir" para juzgar la significación aproximada de los efectos. La carta también puede usarse en sentido inverso. Por ejemplo, suponga que estuviera en duda si el factor 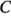es significativo o no. Entonces el experimentador podría preguntar si es razonable esperar que 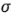pudiera ser tan grande como 10 o más. Si es improbable que 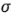sea tan grande como 10, entonces puede concluirse que 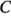es significativo.

Se presentan ahora tres ilustrativos ejemplos de diseños factoriales 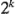no replicados.

Los residuales de un diseño 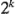proporcionan mucha información acerca del problema bajo estudio. Puesto que los residuales pueden considerarse como los valores observados del ruido o error, con frecuencia ofrecen información acerca de la variabilidad del proceso. Puede hacerse el examen sistemático de los residuales de un diseño 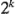no replicado para proporcionar información acerca de la variabilidad del proceso.

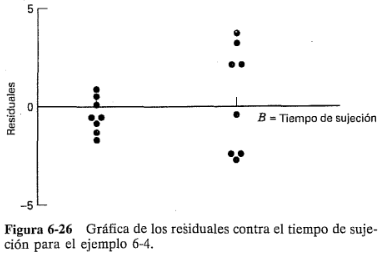
Considere la gráfica de los residuales de la figura 6-26. La desviación estándar de los ocho residuales donde 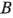 está en el nivel bajo es 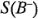= 0.83, y la desviación estándar de los ocho residuales donde  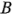está en el nivel alto es 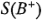= 2.72. El estadístico:

tiene una distribución aproximadamente normal cuando las dos varianzas 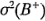y 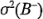son iguales.

Para ilustrar los cálculos, el valor de 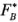es:

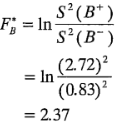
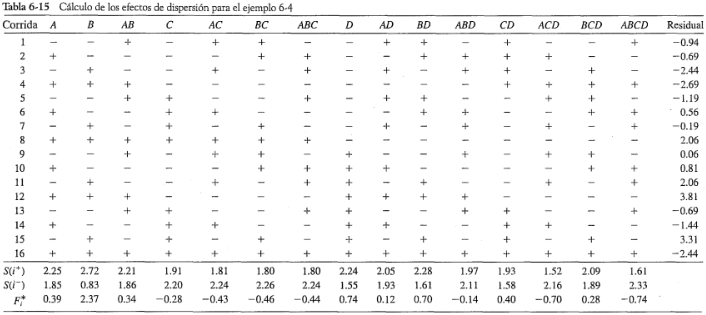
En la tabla 6-15 se presenta el conjunto completo de contrastes para el diseño 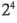junto con los residuales para cada corrida del experimento del proceso de los paneles del ejemplo 6-4. Cada columna de esta tabla contiene el mismo número de signos positivos y negativos, y es posible calcular la desviación estándar de los residuales de cada grupo de signos en cada columna, por ejemplo,  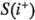y 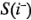, 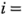1,2, ...,15. Entonces:

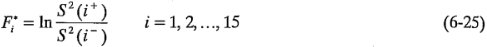
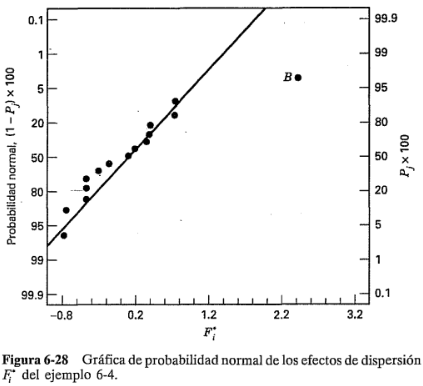
es un estadístico que puede usarse para evaluar la magnitud de los efectos de dispersión del experimento.

Si la varianza de los residuales de las corridas donde el factor 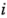 es positivo es igual a la varianza de los residuales de las corridas donde el factor i es negativo, entonces 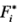tiene una distribución aproximadamente normal. Los valores de 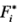se presentan al final de cada columna de la tabla 6-15.

La figura 6-28 es la gráfica de probabilidad normal de los efectos de dispersión 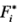. Evidentemente,  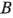es un factor importante en lo que se refiere a la dispersión del proceso. Para un estudio más amplio de este procedimiento, ver Box y Meyer [19] y Myers y Montgomery [85a]. Asimismo, para que los residuales del modelo ofrezcan la información apropiada acerca de los efectos de dispersión, es necesario especificar correctamente el modelo de localización.