6.6.- Adición de puntos centrales en el diseño 2^k

Una preocupación potencial en el uso de diseños factoriales de dos niveles es el supuesto de la linealidad de los efectos de los factores. Desde luego, no es necesaria la linealidad perfecta, y el sistema 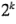 funcionará bastante bien incluso cuando el supuesto de linealidad sea válido sólo de manera muy aproximada. De hecho, se ha señalado ya que, si se agregan los términos de interacción a un modelo de los efectos principales o de primer orden, de donde se obtiene: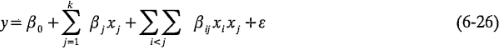

entonces se tiene un modelo con la capacidad de representar cierta curvatura en la función de respuesta. Esta curvatura, desde luego, es resultado del torcimiento del plano inducido por los términos de interacción .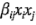

Habrá situaciones en que la curvatura de la función de respuesta no esté modelada adecuadamente por la ecuación 6-26. En tales casos, un modelo lógico por considerar es:

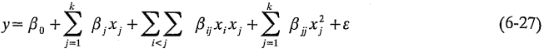
donde las 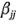representan efectos cuadráticos o de segundo orden puros. A la ecuación 6-27 se le llama modelo de superficie de respuesta de segundo orden.

Cuando se realiza un experimento factorial de dos niveles, por lo general se anticipa el ajuste del modelo de primer orden de la ecuación 6-26, pero deberá estarse alerta ante la posibilidad de que el modelo de segundo orden de la ecuación 6-27 sea en realidad más apropiado. Existe un método para hacer una réplica de ciertos puntos de un diseño factorial 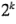 que ofrecerá protección contra la curvatura de los efectos de segundo orden a la vez que permitirá una estimación independiente del error que va a obtenerse. El método consiste en agregar puntos centrales en el diseño 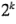. Estos consisten en 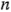réplicas que se corren en los puntos  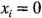( 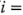1, 2, ..., 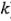). Una razón importante para agregar réplicas de las corridas en el centro del diseño es que los puntos centrales no afectan las estimaciones usuales de los efectos en un diseño 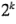. Cuando se agregan puntos centrales, se supone que los 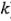factores son cuantitativos.

Para ilustrar este enfoque, considere un diseño 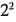con una observación en cada uno de los puntos factoriales (-, -), (+, -), (-, +) y (+, +), y  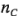observaciones en el punto central (O, O). En la figura 6-34 se ilustra a la situación. Sea  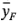el promedio de las cuatro corridas en los cuatro puntos factoriales y sea  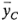el promedio de las  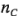corridas en el punto central. Si la diferencia  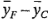es pequeña, entonces los puntos centrales caen en el plano (o cerca de él) que pasa por los puntos factoriales, y no hay curvatura cuadrática. Por otra parte, si  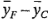es grande, entonces está presente una curvatura cuadrática. La suma de cuadrados de la curvatura cuadrática pura con un solo grado de libertad está dada por:

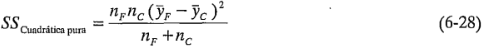
donde, en general, 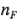es el número de puntos del diseño factorial. Esta cantidad puede compararse con el cuadrado medio del error para probar la curvatura cuadrática pura. Más específicamente, cuando se agregan puntos en el centro del diseño 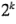con la prueba de la curvatura (utilizando la ecuación 6-28) en realidad se prueban las hipótesis:

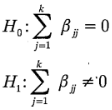
Además, si los puntos factoriales del diseño no tienen réplicas, pueden usarse los 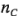puntos centrales para construir una estimación del error con 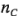- 1 grados de libertad.

En el ejemplo 6-6 se llegó a la conclusión de que no había indicios de efectos cuadráticos; es decir, un modelo de primer orden: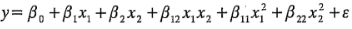

es apropiado (aun cuando probablemente no se necesite el término de la interacción). Habrá situaciones en las que se necesitarán los términos cuadráticos. Es decir, se tendrá que suponer entonces un modelo de segundo orden tal como:

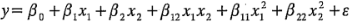
Desafortunadamente, los parámetros desconocidos (las 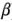) de este modelo no pueden estimarse, ya que hay seis parámetros por estimar y el diseño  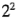más los puntos centrales de la figura 6-35 sólo tienen cinco corridas independientes.

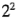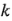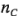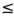
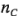
Una solución simple y de gran efectividad de este problema es aumentar el diseño con cuatro corridas axiales, como se ilustra en la figura 6-36a. El diseño resultante, llamado diseño central compuesto, puede usarse entonces para ajustar el modelo de segundo orden. En la figura 6-36b se muestra un diseño central compuesto para = 3 factores. Este diseño tiene 14 + corridas (generalmente 3   5), y es un diseño muy eficiente para ajustar el modelo de segundo orden con 10 parámetros en 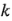=3 factores.

Los diseños compuestos centrales se usan ampliamente para construir modelos de superficie de respuesta de segundo orden. Estos diseños se estudiarán con mayor detalle en el capítulo 11.

Se concluye esta sección con algunas sugerencias y observaciones adicionales útiles referentes al uso de puntos centrales.

1. Cuando un experimento factorial se lleva a cabo en un proceso en marcha, considere utilizar las condiciones de operación actuales (o de receta) como el punto central del diseño. Esto con frecuencia le asegura al personal de operación que al menos una parte de las corridas del experimento van a realizarse bajo condiciones familiares, y por lo tanto es improbable que los resultados obtenidos (por lo menos para estas corridas) sean peores que los que se obtienen típicamente.

2. Cuando el punto central de un experimento factorial corresponde con las condiciones de operación actuales, el experimentador puede usar las respuestas observadas en el punto central para proporcionar una verificación aproximada de si algo "inusual" ocurrió durante el experimento. Es decir, las respuestas del punto central deberán ser muy similares a las respuestas observadas históricamente en la operación rutinaria del proceso. Con frecuencia el personal de operación llevará una carta de control para monitorear el desempeño del proceso. En ocasiones las respuestas de los puntos centrales pueden graficarse directamente en la carta de control como una verificación de la forma en que estuvo operando el proceso durante el experimento.

3. Considere correr las réplicas del punto central en orden no aleatorio. Específicamente, deberán correrse uno o dos puntos centrales en o cerca del principio del experimento, uno odas cerca de la parte media, y uno o dos cerca del final. Al separar los puntos centrales en el tiempo, el experimentador tiene una verificación aproximada de la estabilidad del proceso durante el experimento. Por ejemplo, si ha ocurrido una tendencia en la respuesta mientras se realizaba el experimento, graficar las respuestas de los puntos centrales contra el tiempo puede poner de manifiesto esta situación.

4. En ocasiones los experimentos tienen que realizarse en situaciones en las que la información previa acerca de la variabilidad del proceso es escasa o nula. En estos casos, correr dos o tres puntos centrales como las primeras corridas en el experimento puede ser de suma utilidad. Estas corridas pueden proporcionar una estimación preliminar de la variabilidad. Si la magnitud de la variabilidad parece razonable, se continúa; por otra parte, si la variabilidad observada es mayor que la anticipada (io que la razonable!), habrá que detenerse. Con frecuencia es muy provechoso estudiar la cuestión de por qué es tan grande la variabilidad antes de proceder con el resto del experimento.

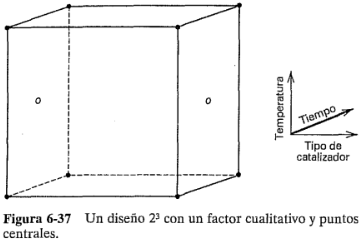
5. Generalmente, se utilizan puntos centrales cuando todos los factores del diseño son cuantitativos. Sin embargo, en ocasiones habrá una o más variables cualitativas o categóricas y varias cuantitativas. Sigue siendo posible emplear los puntos centrales en estos casos. Para ilustrar este punto, considere un experimento con dos factores cuantitativos, el tiempo y la temperatura, cada uno con dos niveles, y un solo factor cualitativo, el tipo de catalizador, también con dos niveles (orgánico e inorgánico). En la figura 6-37 se muestra el diseño 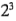para estos factores. Observe que los puntos centrales se colocan en las caras opuestas del cubo que incluyen los factores cuantitativos. En otras palabras, los puntos centrales pueden correrse con las combinaciones de los tratamientos en los niveles alto y bajo de los factores cualitativos, siempre y cuando esos subespacios incluyan únicamente factores cuantitativos.