10.8.- Prueba de Falta de Ajuste

En la sección 6-6 se indicó cómo agregar puntos centrales a un diseño factorial 2^k le permite al experimentador obtener una estimación del error experimental puro. Esto permite hacer la partición de la suma de cuadrados de los residuales SS_E en dos componentes; es decir,

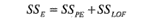
donde SS_PE es la suma de cuadrados debida al error puro y SS_LOF es la suma de cuadrados debida a la falta de ajuste.

Puede presentarse un desarrollo general de esta partición en el contexto de un modelo de regresión. Suponga que se tienen n_i observaciones de la respuesta en el nivel i-ésimo de los regresores x_i, i = 1, 2, ..., m. Sea que y_ij denota la observación j-ésima de1a respuesta en x_i, i = 1, 2, ..., m y j = 1, 2, ..., n_i. Hay n = ∑^m_i=1 n_i observaciones en total. El residual (ij)-ésimo puede escribirse como

donde y'_i es el promedio de las n_i observaciones en x_i. Al elevar al cuadrado ambos miembros de la ecuación 10-56 y hacer la operación suma sobre i y j se obtiene

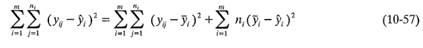
El primer miembro de la ecuación 10-57 es la suma de cuadrados de los residuales ordinaria. Los dos componentes del segundo miembro miden el error puro y la falta de ajuste. Se observa que la suma de cuadrados del error puro

se obtiene calculando la suma de cuadrados corregida de las observaciones repetidas en cada nivel de x y haciendo después la agrupación en los m niveles de x. Si se satisface el supuesto de la varianza constante, ésta es una medida independiente del modelo del error puro, ya que para calcular SS_PE sólo se usa la variabilidad de las y en cada nivel x_i. Puesto que hay n_i - 1 grados de libertad del error puro en cada nivel x_i, el número total de grados de libertad asociados con la suma de cuadrados del error puro es

La suma de cuadrados de la falta de ajuste

es una suma ponderada de los cuadrados de las desviaciones entre la respuesta media y_i en cada nivel x_i, y el valor ajustado correspondiente. Si los valores ajustados y_i están cerca de las respuestas promedio y_i correspondientes, entonces hay un fuerte indicio de que la función de regresión es lineal. Si las y_i se desvían mucho de las y_i, entonces es probable que la función de regresión no sea lineal. Hay m - p grados de libertad asociados con SS_LOF porque hay m niveles de x, y se pierden p grados de libertad porque deben estimarse p parámetros para el modelo. En lo que a los cálculos se refiere, por lo general SS_LOF se obtiene restando SS_PE de SS_E.

El estadístico de prueba para la falta de ajuste es

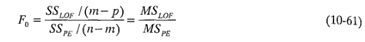
El valor esperado de MS_PE es σ², y el valor esperado de MS_LOF es

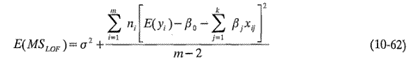
Si la verdadera función de regresión es lineal, entonces E(y_i)=β₀+∑^k_j=1β_jx_ij, y el segundo término de la ecuación 10-62 es cero, dando como resultado E(MS_LOF) = σ². Sin embargo, si la verdadera función de regresión no es lineal, entonces E(y_i)≠β₀+∑^k_j=1β_jx_ij y E(MS_LOF)>σ². Además, si la verdadera función de regresión es lineal, entonces el estadístico F₀ sigue la distribución F_m-p,n-m. Por lo tanto, para probarla falta de ajuste, se calcularía el estadístico de prueba F₀ y se concluiría que la función de regresión no es linealsi F₀ > F_{a, m-p,n-m}.

Es sencillo incorporar este procedimiento de prueba en el análisis de varianza. Si se concluye que la función de regresión no es lineal, entonces el modelo tentativo habrá de abandonarse y deberán hacerse intentos para encontrar una ecuación más apropiada. De manera alternativa, si F₀ no excede F_{a, m-p,n-m}, no existe evidencia sólida de falta de ajuste y MS_PE y MS_LOF se combinan con frecuencia para estimar σ². El ejemplo 6-6 es una ilustración muy completa de este procedimiento, donde las réplicas de las corridas son puntos centrales de un diseño factorial 2².