11.3.2.- Caracterización de la Superficie de Respuesta
Una vez que se ha encontrado el punto estacionario, generalmente es necesario caracterizar la superficie de respuesta en la vecindad inmediata de este punto. Por caracterizar se entiende determinar si el punto estacionario es el punto de una respuesta máxima, mínima o un punto silla. Por lo general también se desea estudiar la sensibilidad relativa de la respuesta a las variables x1, x2, ..., xk.
Como ya se señaló, la forma más directa de hacer esto es examinando una gráfica de contorno del modelo ajustado. Si sólo hay dos o tres variables en el proceso (las x), la construcción e interpretación de esta gráfica de contorno es relativamente sencilla. Sin embargo, incluso cuando hay un número relativamente reducido de variables, un análisis más formal, llamado análisis canónico, puede ser útil.
Es conveniente transformar primero el modelo en un nuevo sistema de coordenadas con el origen en el punto estacionario x, y después hacer la rotación de los ejes de este sistema hasta que sean paralelos a los ejes principales de la superficie de respuesta ajustada. Esta transformación se ilustra en la figura 11-9.
Puede demostrarse que se obtiene así el modelo ajustado
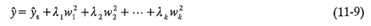
donde las {w¡} son las variables independientes transformadas y las {λ¡} son constantes. A la ecuación 11-9 se le llama la forma canónica del modelo. Además, las {λ¡} son sólo eigenvalores o raíces características de la matriz B.
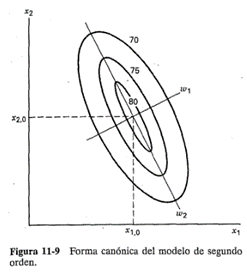
La naturaleza de la superficie de respuesta puede determinarse a partir del punto estacionario y de los signos y magnitudes de las {λ¡}. Primero suponga que el punto estacionario está dentro de la región de exploración para ajustar el modelo de segundo orden. Si todas las {λ¡} son positivas, xs es un punto de respuesta mínima; si todas las {λ¡} son negativas, xs es un punto de respuesta máxima; y si las {λ¡} tienen signos diferentes, xs es un punto silla. Además, la superficie presenta una inclinación mayor en la dirección w¡ para la que |λ¡| es el máximo. Por ejemplo, la figura 11-9 describe un sistema para el que xs es un máximo (λ1 y λ2 son negativas) con |λ1| > |λ2|.
EJEMPLO 11-2
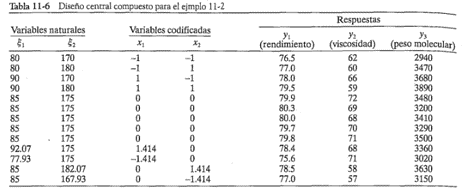
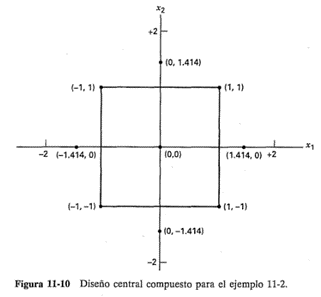
Se continuará el análisis del proceso químico del ejemplo 11-1. No es posible ajustar un modelo de segundo orden en las variables x1 y x2 utilizando el diseño de la tabla 11-4. El experimentador decide aumentar este diseño con puntos suficientes para ajustar un modelo de segundo orden. Obtiene cuatro observaciones en (x1=0, (x2=±1.414) y (x1=±1.414, x2=0). El experimento completo se muestra en la tabla 11-6, y el diseño se ilustra en la figura 11-10. A este diseño se le llama diseño central compuesto (o DCC), el cual se estudiará con mayor detalle en la sección 11-4.2. En esta segunda fase del estudio, dos respuestas adicionales fueron de interés, la viscosidad y el peso molecular del producto. Las respuestas también se muestran en la tabla 11-6.
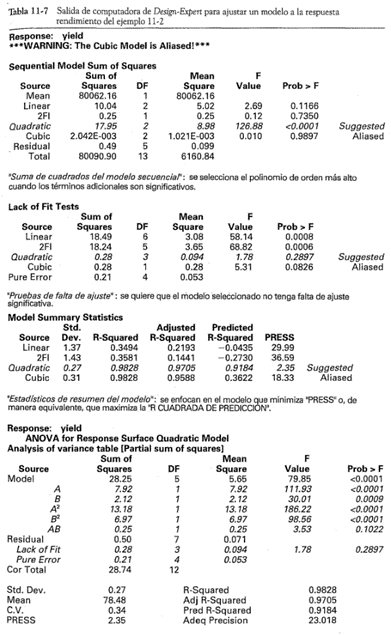
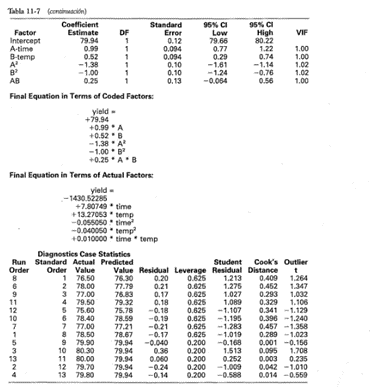
La atención se centrará en el ajuste de un modelo cuadrático para la respuesta rendimiento y1 (las otras respuestas se analizarán en la sección 11-3.4). Por lo general se utiliza software de computadora para ajustar una superficie de respuesta y construir las gráficas de contorno. La tabla 11-7 contiene la salida de Design-Expert. Al examinar la tabla se observa que este paquete de software calcula primero las "sumas de cuadrados extra o secuenciales" de los términos lineales, cuadráticos y cúbicos del modelo (hay un mensaje de advertencia referente a los alias del modelo cúbico, ya que el DCC no contiene corridas suficientes para apoyar un modelo cúbico completo). Con base en el valor P pequeño de los términos cuadráticos, se decide ajustar un modelo de segundo orden a la respuesta rendimiento. La salida de computadora muestra el modelo final en términos tanto de las variables codificadas como de los niveles naturales o reales de los factores.
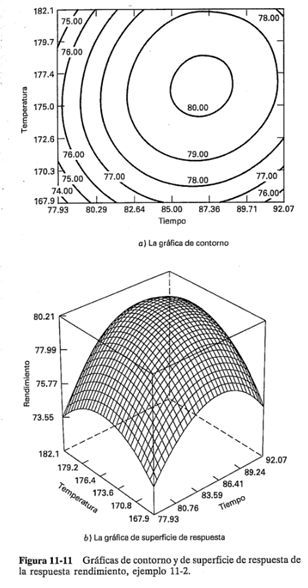
En la figura 11-11 se muestra la gráfica de la superficie de respuesta tridimensional y la gráfica de contorno para la respuesta rendimiento en términos de las variables del proceso tiempo y temperatura. Es relativamente sencillo ver por el examen de estas figuras que el óptimo se encuentra muy cerca de 175 °F y 85 minutos de tiempo de reacción y que la respuesta está en un máximo en este punto. Por el examen de la gráfica de contorno se observa que el proceso puede ser ligeramente más sensible a los cambios en el tiempo de reacción que a los cambios en la temperatura.
La localización del punto estacionario también podría encontrarse utilizando la solución general de la ecuación 11-7. Observe que
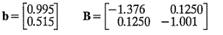
y, por la ecuación 11-7, el punto estacionario es
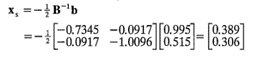
Es decir, x1,s=0.389 y x2,s =0.306. En términos de las variables naturales, el punto estacionario es
.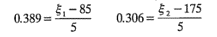
de donde se obtienes Ɛ1 =86.95 =87 minutos de tiempo de reaccióny Ɛ2 =176.53 = 176,5 °F. Este valor está muy cerca del punto estacionario que se encontró por examen visual en la gráfica de contorno de la figura 11-11. Al utilizar la ecuación 11-8, la respuesta predicha en el punto estacionario puede encontrarse como y's = 80.21.
El análisis canónico que se describe en esta sección también puede usarse para caracterizar la superficie de respuesta. Primero es necesario expresar el modelo ajustado en la forma canónica (ecuación 11-9). Los eigenvalores λ1 y λ2 son las raíces de la ecuación de determinantes
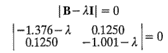
que se reduce a
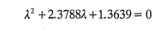
Las raíces de esta ecuación cuadrática son λ1 = -0.9641 y λ2 = -1.4147. Por lo tanto, la forma canónica del modelo ajustado es
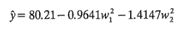
Puesto que tanto λ1 como λ2 son negativas y el punto estacionario está en la región de exploración, se concluye que el punto estacionario es un máximo.
En algunos problemas MSR puede ser necesario encontrar la relación entre las variables canónicas {w¡} y las variables del diseño {x¡}. Esto es particularmente cierto cuando es imposible operar el proceso en el punto estacionario. Como una ilustración, suponga que en el ejemplo 11-2 el proceso no pudo operarse en Ɛ1= 87 minutos y Ɛ2= 176.5 °F debido a que esta combinación de factores resulta en un costo excesivo. Se quiere "regresar" ahora del punto estacionario a un punto con un costo menor sin incurrir en pérdidas considerables en el rendimiento. La forma canónica del modelo indica que la superficie es menos sensible a la pérdida de rendimiento en la direcciónwl . La exploración de la forma canónica requiere convertir los puntos del espacio (w1, w2) en puntos del espacio (x1, x2).
En general, las variables x se relacionan con las variables canónicas w por
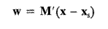
donde M es una matriz ortogonal (k x k). Las columnas de M son los eigenvectores normalizados asociados con {λi}. Es decir, si mi es la columna i-ésima de M, entonces mi es la solución de

para la que ∑kj=1m2ji= 1.
El procedimiento se ilustra usando el modelo de segundo orden ajustado del ejemplo 11-2. Para λ1 =-0.9641, la ecuación 11-10 queda como
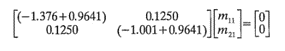
o
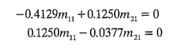
Quiere obtenerse la solución normalizada de estas ecuaciones, es decir, aquella para la que m211+m221=1.
No existe una solución única para estas ecuaciones, por lo que lo más conveniente es asignar un valor arbitrario a una de las incógnitas, resolver elsistemay normalizar la solución. Al hacer m'21=1, se encuentra m'11=0.3027. Para normalizar esta solución, m'11 y m'21 se dividen entre
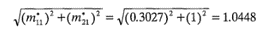
Se obtiene así la solución normalizada
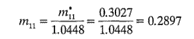
y
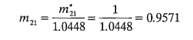
que es la primera columna de la matriz M.
Utilizando λ2 = -1.4147 puede repetirse el procedimiento anterior, obteniéndose m12 = -0.9574 y m22 = 0.2888 como la segunda columna de M. Por lo tanto, se tiene
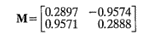
La relación entre las variables w y x es
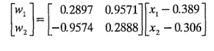
o
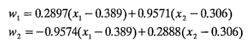
Si quisiera explorarse la superficie de respuesta en la vecindad del punto estacionario, podrían determinarse los puntos apropiados en los cuales hacer las observaciones en el espacio (w1, w2) Yusar después la relación anterior para convertir estos puntos en el espacio (x1, x2) para que puedan realizarse las corridas.
