11.4.3.- Formación de Bloques en los Diseños de Superficie de Respuesta

Cuando se usan diseños de superficie de respuesta, con frecuencia es necesario considerar la formación de bloques para eliminar las variables perturbadoras. Por ejemplo, este problema puede ocurrir cuando un diseño de segundo orden se ensambla secuencialmente a partir de un diseño de primer orden, como se ilustró en los ejemplos 11-1 y 11-2. Puede transcurrir tiempo considerable entre que se corre el modelo de primer orden y se corren los experimentos complementarios requeridos para construir un diseño de segundo orden, y durante este tiempo las condiciones de prueba pueden cambiar, haciendo necesaria la formación de bloques.

Se dice que un diseño de superficie de respuesta se forma de bloques ortogonales si se divide en bloques tales que sus efectos no afecten las estimaciones de los parámetros del modelo de superficie de respuesta. Si se usa un diseño 2^k o 2^k-p como un diseño de superficie de respuesta de primer orden, pueden usarse los métodos del capítulo 7 para disponer las corridas en 2^r bloques. Los puntos centrales de estos diseños deberán asignarse por igual entre los bloques.

Para hacer la formación de bloques ortogonales de un diseño de segundo orden, deben satisfacerse dos condiciones. Si hay n_b observaciones en el bloque b-ésimo, entonces estas condiciones son

     1. Cada bloque debe ser un diseño ortogonal de primer orden; es decir,

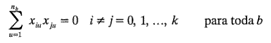
donde x_iu y x_ju son los niveles de las variables i-ésima y j-ésima en la corrida u-ésima del experimento con x_0u = 1 para toda u.

     2. La fracción de la suma de cuadrados total para cada variable con que contribuye cada bloque, debe ser igual a la fracción de las observaciones totales que están contenidas en el bloque; es decir,

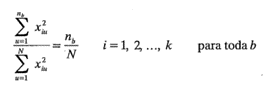
donde N es el número de corridas del diseño.

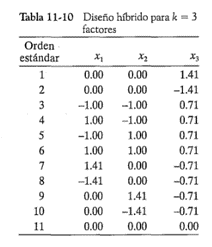
Como un ejemplo de la aplicación de estas condiciones, considere un diseño central compuesto rotable en k =2 variables con N =12 corridas. Los niveles x₁ y x₂ de este diseño pueden escribirse en la matriz del diseño

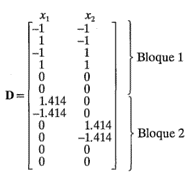
Observe que el diseño se ha dispuesto en dos bloques, con el primer bloque consistiendo en la porción factorial del diseño más dos puntos centrales y el segundo bloque consistiendo en los puntos axiales más dos puntos centrales adicionales. Es claro que la condición 1 se satisface; es decir, ambos bloques son diseños de primer orden ortogonales. Para investigar la condición dos, considere primero el bloque 1 y observe que 

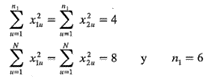
Por lo tanto,

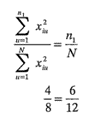
Así, la condición 2 se satisface en el bloque 1. Para el bloque 2 se tiene

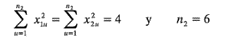
Por lo tanto,

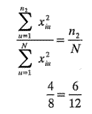
Puesto que la condición 2 también se satisface en el bloque 2, este diseño está formado de bloques ortogonales.

En general, el diseño central compuesto siempre puede construirse para hacer la formación de bloques ortogonales en dos bloques con el primer bloque consistiendo en n_F puntos factoriales más n_CF puntos centrales y el segundo bloque consistiendo en n_A = 2k puntos axiales más n_CA puntos centrales. La primera condición de la formación de bloques ortogonales se cumplirá siempre independientemente del valor que se use para α en el diseño. Para que la segunda condición se cumpla,

El miembro izquierdo de la ecuación 11-15 es α²/n_F, y después de sustituir esta cantidad, la ecuación para el valor de α que resultará en la formación de bloques ortogonales puede resolverse como

Este valor de a no dará como resultado, en general, un diseño rotable o esférico. Si se requiere que el diseño también sea rotable, entonces α = (n_F)^1/4 y

No siempre es posible encontrar un diseño que satisfaga exactamente la ecuación 11-17. Por ejemplo, si k = 3, n_F = 8 y n_A = 6, la ecuación 11-17 se reduce a

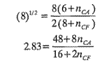
Es imposible encontrar valores de n_CA y n_CF que satisfagan exactamente esta última ecuación. Sin embargo, observe que si n_CF = 3 y n_CA = 2, entonces el segundo miembro es

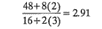
por lo que el diseño se separa en bloques casi ortogonales. En la práctica podría relajarse un tanto el requerimiento de la rotabilidad o bien el de la formación de bloques ortogonales sin ninguna pérdida importante de información.

El diseño central compuesto es muy versátil en cuanto a su capacidad para incorporar la formación de bloques. Si k es lo suficientemente grande, la porción factorial del diseño puede dividirse en dos o más bloques. (El número de bloques factoriales debe ser una potencia de 2, con la porción axial formando un solo bloque.) En la tabla 11-11 se presentan varias disposiciones útiles de la formación de bloques para el diseño central compuesto.

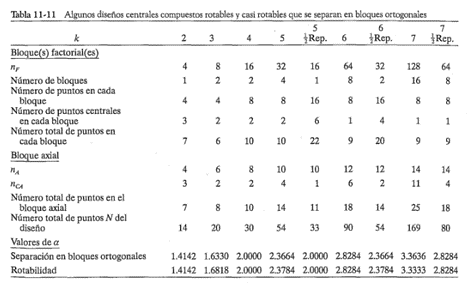
Cabe destacar dos puntos importantes acerca del análisis de varianza cuando el diseño de superficie de respuesta se ha corrido en bloques. El primero se refiere al uso de los puntos centrales para calcular una estimación del error puro. Sólo los puntos centrales que se corren en el mismo bloque pueden considerarse como réplicas, por lo que el término del error puro sólo puede calcularse dentro de cada bloque. Si la variabilidad es consistente en todos los bloques, entonces estas estimacionesdel error puro podrían agruparse. El segundo punto se refiere al efecto de bloque. Si el diseño se forma de bloques ortogonales en m bloques, la suma de cuadrados de los bloques es

donde B_b es el total de las n_b observaciones en el bloque b-ésimo y G es el gran total de las N observaciones en los m bloques. Cuando los bloques no son exactamente ortogonales, puede usarse la prueba general de significación de la regresión (el método de la "suma de cuadrados extra") que se describió en el capítulo 10.