11.8.- Problemas

11-1. En una planta química se produce oxígeno licuando aire y separándolo por destilación fraccionada en sus gases componentes. La pureza del oxígeno es una función de la temperatura del condensador principal y de la relación de la presión entre las columnas superior e inferior. Las condiciones de operación actuales son temperatura (Ɛ₁) = -220°Cy la relación de la presión (Ɛ₂) = 1.2. Utilizando los datos siguientes, encontrar la trayectoria del ascenso más pronunciado:

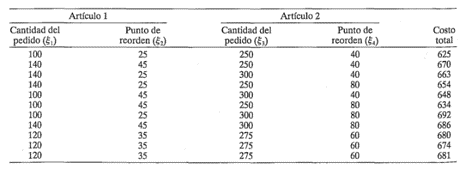
11-2. Un ingeniero industrial ha desarrollado un modelo de simulación por computadora para un sistema de inventario de dos artículos. Las variables de decisión son la cantidad del pedido y el punto de reorden de cada artículo. La respuesta que debe minimizarse es el costo total del inventario. El modelo de simulación se usa para producir los datos que se muestran en la tabla siguiente. Identificar el diseño experimental. Encontrar la trayectoria del descenso más pronunciado.

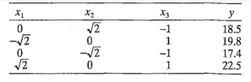
11-3. Verificar que el siguiente diseño es símplex. Ajustar el modelo de primer orden y encontrarla trayectoria del ascenso más pronunciado.

11-4. Para el modelo de primer orden

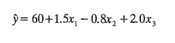
encontrarla trayectoria del ascenso más pronunciado. Las variables están codificadas como -1≤x_i≤1.

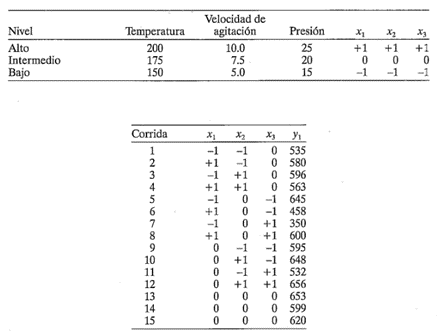
11-5. La región de experimentación de tres factores son el tiempo (40≤T₁≤80 min), la temperatura (200≤T₂≤300°C) y la presión (20≤P≤50 psig). Se ha ajustado un modelo de primer orden en variables codificadas a los datos del rendimiento de un diseño 2³. El modelo es

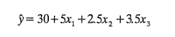
¿El punto T₁ = 85, T₂ = 325, P = 60 está en la trayectoria del ascenso más pronunciado?

11-6. La región de experimentación de dos factores son la temperatura (100≤T≤300°F) y la velocidad de alimentación del catalizador (10≤C≤30 lb/pulg). Un modelo de primer orden con las variables codificadas usuales ±1 se ha ajustado a la respuesta peso molecular, obteniéndose el modelo siguiente:

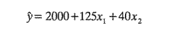
     a) Encontrar la trayectoria del ascenso más pronunciado.

     b) Se desea mover a una región donde los pesos moleculares rebasen 2500. Con base en la información que se tiene por la experimentación en esta región, ¿aproximadamente cuántos pasos en la trayectoria del ascenso más pronunciado se necesitan para moverse a la región de interés?

11-7. La trayectoria del ascenso más pronunciado suele calcularse suponiendo que el modelo es en realidad de primer orden; es decir, que no hay interacción. Sin embargo, incluso si hay interacción, el ascenso más pronunciado que se determina ignorando la interacción seguirá produciendo por lo general buenos resultados. Para ilustrar, suponga que se ha ajustado el modelo

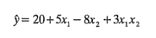
utilizando variables codificadas (-1≤x_i≤1).

     a) Trazar la trayectoria del ascenso más pronunciado que se obtendría si se ignorara la interacción.

     b) Trazar la trayectoria del ascenso más pronunciado que se obtendría incluyendo la interacción en el modelo. Compararla con la trayectoria que se encontró en el inciso a.

11-8. Los datos que se muestran en la siguiente tabla se recolectaron en un experimento para optimizar el crecimiento de un cristal como una función de tres variables x₁, x₂ y x₃. Son deseables los valores grandes dey (rendimiento en gramos). Ajustar un modelo de segundo orden y analizar la superficie ajustada. ¿Bajo qué conjunto de condiciones se alcanza el crecimiento máximo?

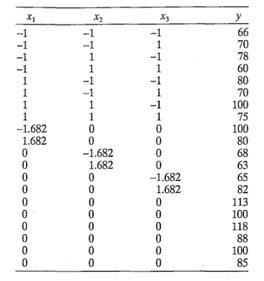
11-9. Un ingeniero químico recolectó los siguientes datos. La respuesta y es el tiempo de filtración, x₁ es la temperatura y x₂ es la presión. Ajustar un modelo de segundo orden.

     a) ¿Qué condiciones de operación se recomendarían si el objetivo es minimizar el tiempo de filtración?

     b) ¿Qué condiciones de operación se recomendarían si el objetivo es operar el proceso con una velocidad de filtración media muy próxima a 46?

11-10. El diseño hexagonal que se presenta a continuación se usa en un experimento que tiene como objetivo ajustar un modelo de segundo orden:

     a) Ajustar el modelo de segundo orden.

     b) Efectuar el análisis canónico. ¿Qué tipo de superficie se ha encontrado?

     c) ¿Qué condiciones de operación para x₁ y x₂ llevan al punto estacionario?

     d) ¿Dónde se correría este proceso si el objetivo es obtener una respuesta que esté tan cerca de 65 como sea posible?

11-11. Un experimentador corrió un diseño de Box-Behnken y obtuvo los siguientes resultados, donde la variable de respuesta es la viscosidad de un polímero:

     a) Ajustar el modelo de segundo orden.

     b) Efectuar el análisis canónico. ¿Qué tipo de superficie se ha encontrado?

     c) ¿Qué condiciones de operación para x₁, x₂ y x₃ llevan al punto estacionario?

     d) ¿Qué condiciones de operación se recomendarían si es importante obtener una viscosidad que esté tan cerca de 600 como sea posible?

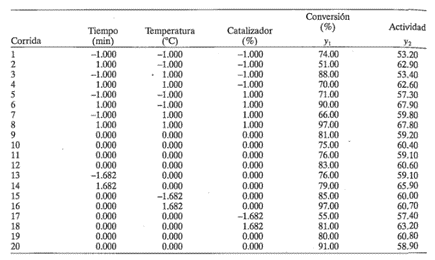
11-12. Considere el diseño central compuesto de tres variables que se muestra a continuación. Analizar los datos y sacar conclusiones, suponiendo que se quiere maximizarla conversión (y₁) con la actividad (y₂) entre 55 y 60.

11-13. Un fabricante de herramientas de corte ha desarrollado dos ecuaciones empíricas para la vida de la herramienta en horas (y₁) y para el costo de la herramienta en dólares (y₂). Ambos modelos son funciones lineales de la dureza del acero (x₁) y de la fecha de fabricación (x₂). Las dos ecuaciones son

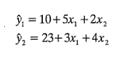
y ambas ecuaciones son válidas en el rango -1.5≤x_i≤1.5. El costo unitario de la herramienta debe estar abajo de $27.50 y la vida debe exceder 12 horas para que el producto sea competitivo. ¿Existe algún conjunto de condiciones de operación factible para este proceso? ¿Dónde se recomendaría correr este proceso?

11-14. Se corre un diseño central compuesto eh un proceso de deposición química por vapor y se obtienen los datos experimentales que se muestran a continuación. Se procesaron simultáneamente cuatro unidades experimentales en cada corrida del diseño, y las respuestas son la media y la varianza del espesor, calculadas en las cuatro unidades.

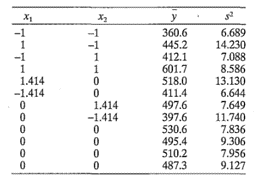
     a) Ajustar un modelo a la respuesta media. Analizar los residuales.

     b) Ajustar un modelo a la respuesta varianza. Analizar los residuales.

     c) Ajustar un modelo a ln(s²). ¿Este modelo es superior al que se encontró en el inciso b?

     d) Suponga que se quiere que el espesor medio esté en el intervalo 450 ± 25. Encontrar un conjunto de condiciones de operación que consiga este objetivo y que al mismo tiempo minimice la varianza.

     e) Comentar los aspectos de la minimización de la varianza del inciso d. ¿Se ha minimizado también la varianza total del proceso?

11-15. Verificar que el diseño de primer orden ortogonal es también un diseño de primer orden rotable.

11-16. Demostrar que aumentar un diseño 2^k con n_c puntos centrales no afecta las estimaciones de β_¡(i = 1,2, ..., k), pero que la estimación de la ordenada al origen β₀ es el promedio de las 2^k + n_c observaciones.

11-17. El diseño central compuesto rotable. Puede demostrarse que un diseño de segundo orden es rotable si ∑ⁿ_u=1x^a_iux^b_ju=0 si a o b (o ambas) son impares y si ∑ⁿ_u=1x⁴_iu=3∑ⁿ_u=1x²_iux²_ju. Demostrar que para el diseño central compuesto estas condiciones llevan a α= (n_F)^1/4 para la rotabilidad, donde n_F es el número de puntos en la porción factorial.

11-18. Verificar que el diseño central compuesto que se muestra abajo está separado en bloques ortogonales:

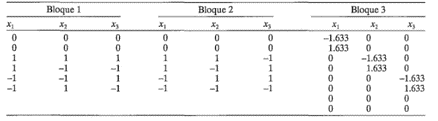
11-19. Formación de bloques del diseño central compuesto. Considere un diseño central compuesto para k = 4 variables en dos bloques. ¿Puede encontrarse siempre un diseño rotable formado de bloques ortogonales?

11-20. ¿Cómo puede correrse un diseño hexagonal en dos bloques ortogonales?

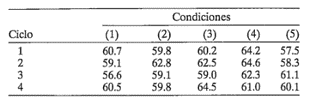
11-21. En la tabla siguiente se muestra el rendimiento durante los cuatro primeros ciclos de un proceso químico. Las variables son el porcentaje de concentración (x₁) en los niveles 30, 31 y 32 y la temperatura (x₂) en 140, 142 y 144°F. Hacer el análisis utilizando métodos EVOP.

11-22. Suponga que se aproxima una superficie de respuesta con un modelo de orden d₁, tal como y = X₁β₁ + Ɛ, cuando la verdadera superficie está descrita por un modelo de orden d₂>d₁; es decir, E(y) = X₁β₁ + X₁β₂.

     a) Demostrar que los coeficientes de regresión son sesgados, es decir, que E(β'₁)=β₁+Aβ₂, donde A=(X'₁X₁)^-1X'₁X₂. Es común llamar a A la matriz alias.

     b) Si d₁ = 1 y d₂ = 2, y se utiliza un diseño 2^k completo para ajustar el modelo, usar el resultado del inciso a para determinar la estructura de los alias.

     c) Si d₁ = 1, d₂ = 2 y k = 3, encontrar la estructura de los alias, suponiendo que se usa un diseño 2^3-1 para ajustar el modelo.

     d) Si d₁ = 1, d₂ = 2 y k = 3, Yse utiliza el diseño símplex del problema 11-3 para ajustar el modelo, determinar la estructura de los alias y comparar los resultados con el inciso c.

11-23. En un artículo ("Conozcamos todos el cuadrado latino", en Quality Engineeling, vol. 1, pp. 453-465), J.S. Hunter ilustra algunos de los problemas asociados con los diseños factoriales fraccionados 3^{k -p}. El factor A es la cantidad de etanol agregada a un combustible estándar y el factor B representa la: relación aire/combustible. La variable de respuesta es la emisión de monóxido de carbono (CO) en g/m³. El diseño se muestra abajo:

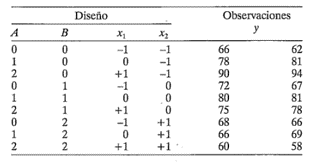
Observe que se ha usado el sistema de notación de 0, 1 y 2 para representar los niveles bajo, intermedio y alto de los factores. Se ha usado también una "notación geométrica" de -1, 0 y +1. Se hacen dos réplicas de cada corrida del diseño.

     a) Verificar que el modelo de segundo orden

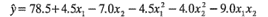
es un modelo razonable para este experimento. Trazar los contornos de la concentración de CO en el espacio x₁, x₂.

     b) Suponga ahora que en lugar de sólo dos factores, se usaron cuatro factores en un diseño factorial fraccionado 3^4-2 y que se obtuvieron exactamente los mismos datos que en el inciso a. El diseño sería el siguiente:

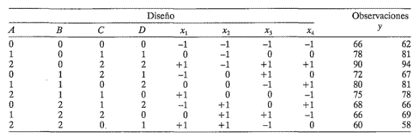
Confirmar que este diseño es un arreglo ortogonal L₉.

     c) Calcular los promedios marginales de la respuesta CO en cada nivel de los cuatro factores A, B, C y D. Construir gráficas de estos promedios marginales e interpretar los resultados. ¿Los factores C y D parecen tener efectos grandes? ¿Estos factores tienen en realidad algún efecto sobre la emisión de CO? ¿Por qué su efecto aparente es grande? .

     d) El diseño del inciso b permite el ajuste del modelo

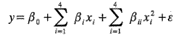
Suponga que el verdadero modelo es

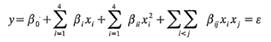
Demostrar que si las β'_j representan las estimaciones de mínimos cuadrados de los coeficientes del modelo ajustado, entonces

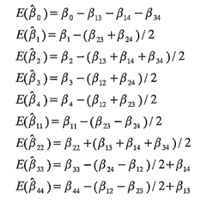
Ayuda esto a explicar los efectos grandes de los factores C y D que se observaron gráficamente en el inciso c?

11-24. Suponga que es necesario diseñar un experimento para ajustar un modelo cuadrático en la región -1≤x_i≤+1, i=1,2 sujeto a la restricción x₁+x₂≤1. Si se viola la restricción, el proceso no funcionará adecuadamente. No es posible hacer más de n=12 corridas. Establecer los siguientes diseños:

     a) Un modelo DCC "inscrito" con punto central en x₁=x₂= 0.

     b) Un diseño factorial 3² "inscrito" con punto central en x₁=x₂= -0.25.

     c) Un diseño optimal D.

     d) Un diseño optimal D modificado que sea idéntico al del inciso c, pero con todas las réplicas de las corridas en el centro del diseño.

     e) Evaluar el criterio |(X'X)^-1| para cada diseño.

     f) Evaluar la eficiencia D para cada diseño en comparación con el diseño optimal D del inciso c.

     g) ¿Qué diseño preferiría el lector? ¿Por qué?

11-25. Considere un diseño 2³ para ajustar un modelo de primer orden.

     a) Evaluar el criterio D|(X'X)^-1| para este diseño.

     b) Evaluar el criterio A tr(X'X)^-1 para este diseño.

     c) Encontrar la varianza de predicción escalada máxima para este diseño. ¿Este diseño es optimal G?

11-26. Repetir el problema 11-25 utilizando un modelo de primer orden con las interacciones de dos factores.

11-27. Un ingeniero químico desea ajustar una curva de calibración para un nuevo procedimiento utilizado para medir la concentración de un ingrediente particular de un producto fabricado en sus instalaciones. Pueden prepararse 12 muestras, cuya concentración es conocida. El ingeniero quiere construir un modelo para las concentraciones medidas. Piensa que una curva de calibración lineal será adecuada para modelar la concentración medida como una función de las concentraciones conocidas; es decir, y = β₀+β₁x+Ɛ, donde x es la concentración real. Están bajo consideración cuatro diseños experimentales. El diseño 1 consta de seis corridas con la concentración conocida 1 y seis corridas con la concentración conocida 10. El diseño 2 consta de cuatro corridas con las concentraciones 1, 5.5 y 10. El diseño 3 consta de tres corridas con las concentraciones 1,4,7 y 10. Por último, el diseño 4 consta de tres corridas con las concentraciones 1 y 10 y seis corridas con la concentración 5.5.

     a) Graficar la varianza de predicción escalada para los cuatro diseños en la misma gráfica en el rango de la concentración 1≤x≤10. ¿Qué diseño sería preferible?

     b) Calcular el determinante de (X'X)^-1 para cada diseño. ¿Qué diseño sería preferible de acuerdo con el criterio D?

     c) Calcular la eficiencia D de cada diseño en comparación con el "mejor" diseño que se haya encontrado en el inciso b.

     d) Para cada diseño, calcular la varianza de predicción promedio en el conjunto de puntos dado por x=1, 1.5, 2, 2.5, ..., 10. ¿Qué diseño sería preferible de acuerdo con el criterio V?

     e) Calcular la eficiencia V de cada diseño en comparación con el mejor diseño que se haya encontrado en el inciso d.

f) ¿Cuál es la eficiencia G de cada diseño?

11-28. Resolver de nuevo el problema 11-27, suponiendo que el modelo que el ingeniero quiere ajustar es cuadrático. Evidentemente, ahora sólo pueden considerarse los diseños 2, 3 y 4.

11-29. Un experimentador quiere correr un experimento de una mezcla de tres componentes. Las restricciones sobre las proporciones de los componentes son las siguientes:

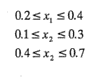
     a) Establecer un experimento para ajustar un modelo cuadrático para mezclas. Usar n = 14 corridas, con cuatro réplicas. Usar el criterio D.

     b) Trazar la región experimental.

     c) Establecer un experimento para ajustar un modelo cuadrático para mezclas con n=12 corridas, suponiendo que tres de estas corridas son réplicas. Usar el criterio D.

     d) Comentar los dos diseños que se encontraron.

11-30. Myers y Montgomery [85a] describen un experimento con una mezcla de gasolina en el que intervienen tres componentes de la mezcla. No hay restricciones sobre las proporciones de la mezcla, y se usó el siguiente diseño con 10 corridas:

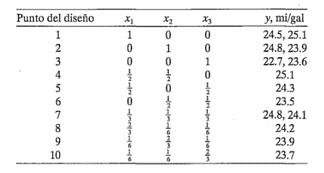
     a) ¿Qué tipo de diseño utilizaron los experimentadores?

     b) Ajustar un modelo cuadrático para mezclas a los datos. ¿Es adecuado este modelo?

     c) Graficar los contornos de la superficie de respuesta. ¿Qué mezcla se recomendaría para maximizar las millas por galón?

11-31. Considere el experimento del llenado de las botellas del ejemplo 6-1. Suponga que el porcentaje de carbonatación (A) es una variable de ruido (en unidades codificadas σ²_z=1).

     a) Ajustar el modelo de respuesta a estos datos. ¿Se trata de un problema de diseño robusto?

     b) Encontrar el modelo de la media y el modelo de la varianza o bien la POE.

     c) Encontrar un conjunto de condiciones que resulten en una desviación del llenado promedio tan próxima a cero como sea posible con varianza transmitida mínima.

11-32. Considere el experimento del problema 11-12. Suponga que la temperatura es una variable de ruido (σ²_z=1 en unidades codificadas). Ajustar modelos de respuesta para las dos respuestas. ¿Se trata de un problema de diseño robusto con respecto a ambas respuestas? Encontrar un conjunto de condiciones que maximicen la conversión con la actividad entre 55 y 60 y que minimice la variabilidad transmitida porla temperatura.

11-33. Se ha corrido un experimento en un proceso que aplica un material de recubrimiento a una oblea. En cada corrida del experimento se fabricó una oblea y se midió varias veces el espesor del recubrimiento en varios sitios de la misma. Después se obtuvo la media y₁ y la desviación estándar y₂ de la medición del espesor. Los datos (adaptados de Box y Draper [16b]) se muestran en la tabla siguiente:

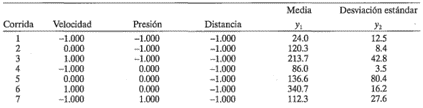
     a) ¿Qué tipo de diseñó utilizaron los experimentadores? ¿Es ésta una buena elección del diseño para ajustar un modelo cuadrático?

     b) Construir los modelos para ambas respuestas.

     c) Encontrar un conjunto de condiciones óptimas que resulten en una media tan grande como sea posible con la desviación estándar menor que 60.

11-34. Una variación del ejemplo 6-2. En el ejemplo 6-2 se encontró que una de las variables del proceso (B = presión) no era importante. Al eliminar esta variable se producen dos réplicas de un diseño 2³. Los datos se muestran enseguida:

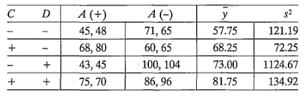
Suponer que C y D son factores controlables y que A es una variable de ruido.

     a) Ajustar un modelo para la respuesta media.

     b) Ajustar un modelo para la respuesta ln(s²).

     c) Encontrar las condiciones de operación que resulten en la respuesta de rapidez de filtración media que exceda 75 con varianza mínima.

     d) Comparar los resultados obtenidos con los del ejemplo 11-6, en el que se aplicó el enfoque de la transmisión del error. ¿Hasta qué punto son similares las dos respuestas?